GF2p8 Аффинные преобразования

Продолжаю тему затронутую в прошлом сообщении. Задача - научиться использовать на практике аффинные преобразования в поле GF2p8.

Пока что можно сказать, что аффинные преобразования предложенные набором инструкций Intel GF-NI реализуют всевозможные сдвиги и реализуют в себе битовые операции исключающее ИЛИ. Любые функции от одного переменного, которые можно представить, как сдвиги и битовое ИЛИ можно предствить этой операцией.

Для освоения операции я предлагаю создать инструментарий, который может использоваться для расчета матриц.
Инструменты такие: cложение матриц, умножение матриц, умножение матрицы на вектор, выделение строки и колонки из матрицы, транспонирование матриц, вычисление обратной матрицы.

Матрицы - это что-то из области линейной алгебры, над матрицами определены операции: сложения и умножения. Алгеброй называем множество матриц 8x8 и операции определенные на этом множестве. Меня заносит в абстрактную алгебру...
Утверждаем существование нейтрального элемента -- единичной диагональной матрицы (E), такой, что умножение на единичную матрицу дает ту же матрицу E·M = M. Вообще-то не все равно, с какой стороны умножать матрицы... Утверждаем существование нейтрального элемента нулевой матрицы (Z) по отношению к операции сложения матриц, M+Z = M.

Утверждаем существование обратной матрицы для каждого элемента - обратная матрица имеет свойство M·M^-1 = E - произведение прямой и обратной матрицы дает нейтральный элемент - единичную диагональную матрицу. Следует также определить обратную операцию и для сложения, M⊕(-M) = Z -- так определим. Обратная матрица по отношению к сложению - та же самая матрица, поскольку базовой операцией для сложения элементов матрицы явдяеься исключающее ИЛИ.

Операции сложения и умножения элементов матрицы определим на множестве состоящем из 0 и 1. Операция сложения - Исключающее ИЛИ, операция умножения - логическое И.

Операция аффинного преобразования, которая соответствует процессорной инструкции GF2p8affine запишем в виде алгоритма, хоть и не поздно записать ее в виде формулы математической, я бы предложил уйти от матричного представления в представление сериализованное в виде шестнацатеричных чисел. Каждая строка матрицы может быть записана в шестнадцатеричном виде и вместе образуют вектор упакованный в 64 бит.

Матричное представление:
11111000 =F8
01111100 =7C
00111110 =3E
00011111 =1F
10001111 =8F
11000111 =C7
11100011 =E3
11110001 =F1

0xF1E3C78F1F3E7CF8 - сериализованное представление 64бит.

Нам понадобятся операции выделения строки(8бит) и столбца(8бит) из матрицы 8x8. Кроме того, понадобится функция, которая позволяет установить столбец и строку в матрице. Мы можем простыми сдвиговыми операциями поместить строку (8бит) в матрицу, в сериальном представлении 64бит, а для помещения строки в столбец нужно выполнить транспонирование матрицы после добавления строки.

// Выделение строки матрицы 8 бит
uint8_t m_row(uint64_t M, int n){
    return M>>(8*(7-n));
}

// Выделение колонки матрицы
uint8_t m_column(uint64_t M, int n){
    uint8_t r=0;
    uint8_t mask = 1<<n;
    int i;
    for (i=0;i<8;i++)
        if((M>>(8*(7-i))) & mask) 
            r |= (1<<i);
    return r;
}

Операцию умножения вектора на матрицу назовем аффинными преобразованиями.

// Аффинные преобразования векторов 8бит.
uint8_t affine_byte(uint64_t M, uint8_t byte, uint8_t inv) {
    uint8_t res = 0;
    int i;
    for (i=0; i < 8; i++) {
        // умножить строку на вектор, побитово:
        uint8_t x = m_row(M,i) & byte;
        // выставить бит в векторе результата 
        res |= parity(x)<<i;
    }
    return res ^ inv;
}

Функция parity - исключающее или от байта результата, в GCC я использовал встроенную псевдофункцию __builtin_parity().

При последовательном применении аффинных преобразований матрица воздействует на вектор 8бит. Это записывается, как произведение матриц - последовательное наложение. Матрицы можно перемножать и результат последовательного наложения матриц преобразования - наложение произведения матриц. Определим операцию умножения матриц.

// Умножение матриц
uint64_t m_mul(uint64_t m1, uint64_t m2)
{
    uint64_t r=0;
    int x,y;
    for (y=0; y<8; y++)
      for (x=0; x<8; x++){
        v  = m_row(m1, y) & m_column(m2, x);
        r |= (uint64_t)parity(v) << ((7-y)*8+x);
      }
    return r;
}

Для операции сложения матриц не нужна отдельная функция, потому что сложение матриц - это побитовая операция исключающее ИЛИ. Для порядка определим функцию, но дальше по тексту будем использовать оператор ^(шляпка).

// Сложение матриц
uint64_t m_add(uint64_t m1, uint64_t m2)
{
	return m1 ^ m2;
}

К матрицам нужно относится аккуратно, как к операторам, оператор воздействует на объект справа от оператора. Операторы нельзя менять местами -- последовательность применения операторов важна. M1·M2 не тоже самое, что M2·M1. Однако, сложение матриц обладает свойством M1⊕M2 = M2⊕M1.

Иногда надо уметь много раз подряд применить одно и то же преобразование. Такая операция напоминает экспоненту и записывается Mⁿ. Преобразование задается матрицей, последовательно применяется несколько таких преобразований. Благодаря линейности операций можно использовать произведение матриц, т.е. уменьшить количество операций в программе за счет объединения матриц.

// Экспонирование матриц
uint64_t m_exp(uint64_t m, int n)
{
    uint64_t r=E;// единичная диагональная матрица
    int i;
    for (i=0;i<n;i++)
        r = m_mul(r,m);
    return r;
}

// транспонирование матрицы 8x8
uint64_t m_transpose(uint64_t m)
{
	uint64_t r = 0;
	int x,y;
	for (y=0; y<8; y++){
		uint8_t row = m>>(8*(7-y));
		for (x=0; x<8; x++){
			if(row & (1<<x))
				r |= 1ULL<<((7-x)*8+y);
		}
	}
	return r;
}

Эффективность реализации этих операций нас не волнует, потому что все эти операции нужны для расчета констант в коде - матриц аффинных преобразований, необходимость расчета динамически в процессе исполнения мне сложно представить.

Базовые операции

В этом разделе предложим некоторый базис операций и соответствующие им матрицы аффинных преобразований. Представленные ниже матрицы можно использовать для построения более сложных операций. Более сложные операции получаются методом последовательного наложения матриц (перемножение матриц) и сложения матриц. При этом сколько бы мы ни складывали матрицы и сколько бы не накладывали - результирующую операцию можно представить матрицей, одна процессорная инструкция с пропускной способностью две инструкции типа gf2p8affine за такт. Основной способ комбинирования базовых операций - наложть (перемножить) последовательно несколько одинаковых матриц или сложить матрицу одной операции с матрицой другой операции от общего аргумента.

0102040810204080₁₆ -- единичная матрица (E), результат без изменения

8040201008040201₁₆ -- отраженный порядок бит.

8001020408102040₁₆ -- циклический сдвиг влево на разряд

M= E>>(8*n) | E<<(8*(8-n)) -- циклический сдвиг влево на n разрядов.

0204081020408001₁₆ -- циклический сдвиг вправо на разряд

M= E<<(8*n) | E>>(8*(8-n)) -- циклический сдвиг вправо на n разрядов.

0204081020408080₁₆ -- арифметический сдвиг вправо на разряд с расширением знака

0001020408102040₁₆ -- сдвиг влево на разряд

889830E858B162C4₁₆ -- сдвиг влево с редуцированием по полиному 0x11B

M=(E>>(8*1)) ^ m_transpose(0x1B)

3849921D03070E1C₁₆ -- сдвиг вправо -уполовинивание по полиному 0x11B

M=(E<<(8*1)) ^ m_transpose((0x11BULL>>1)<<56)

51D022F0946028C0₁₆ -- возведение в квадрат с редуцированием по полиному 0x11B.

Сдвиг с редуцированием - это базовая операция, на которой строится умножение в поле. Для каждого образующего полинома будет своя матрица.

Полиномиальное умножение на константу (умножение без переносов)

Можно предложить две операции умножения, первая операция возвращает - старшие 8 бит, вторая - младшие 8 бит.

Младшая часть умножения на константу P(8 бит)
M=(P&0x01? E>> 0: 0)
 ^(P&0x02? E>> 8: 0)
 ^(P&0x04? E>>16: 0)
 ^(P&0x08? E>>24: 0)
 ^(P&0x10? E>>32: 0)
 ^(P&0x20? E>>40: 0)
 ^(P&0x40? E>>48: 0)
 ^(P&0x80? E>>56: 0);

Старшая часть умножения на константу P(9 бит)
M=(P&0x100? E<< 0: 0)
 ^(P&0x080? E<< 8: 0)
 ^(P&0x040? E<<16: 0)
 ^(P&0x020? E<<24: 0)
 ^(P&0x010? E<<32: 0)
 ^(P&0x008? E<<40: 0)
 ^(P&0x004? E<<48: 0)
 ^(P&0x002? E<<56: 0);

Редуцирование по методу Барретта

Редуцирование предполагает использование двух умножений на константу (Ur, Pr), при этом используется только старшая часть умножения без переноса. Возможно в одной матрице совместить умножение на константу и последующее редуцирование. Или можно предложить операцию, которая на вход принимает старшую часть умножения и выдает результат редуцирования, который надо добавить к младшей части.

Умножение на константу с редуцированием по полиному можно выполнить в одну инструкцию.

B = Mpl·Mbh·Mch·A + Mcl·A = (Mpl·Mbh·Mch + Mcl)·A
A - байт (вектор из 8 бит) над которым производится операция.
Mcl - младшая часть умножения на константу
Mch - старшая часть умножения на константу
Mpl - младшая часть результата умножения без переноса на Pr=0x11B 
Mbh - старшая часть умножения на константу Барретта Ur=0x145
Mpl[0x11B]·Mbh[0x145] -- операция редуцирования по полиному 0x11B. 

Это и есть способ получения матрицы:

M = Mpl·Mbh·Mch + Mcl

Следует перемножить три матрицы в определенной последовательности и добавить четвертую. В результате получаем матрицу аффинного преобразования, которое в одну инструкцию выполняет все эти действия.

Возведение в квадрат

Почему возможно? Причина прозаичная: (A⊕B)² = A² ⊕ B² -- можно независимо считать квадрат каждого двоичного разряда. Для составления матрицы использую тот же принцип - по разрядом, каждый разряд возводится в квадрат независимо. Для старших разрядов выполняется редуцирование по полиному поля (0x11B).

M2=0x0100000000000000ULL// 1^2 = 0x01
  ^0x0000020000000000ULL// 2^2 = 0x04
  ^0x0000000004000000ULL// 4^2 = 0x10
  ^0x0000000000000800ULL// 8^2 = 0x40
  ^0x1010001010000000ULL//     = 0x1B
  ^0x0000202000202000ULL//     = 0x6C
  ^0x4040004000400040ULL//     = 0xAB
  ^0x0080008080000080ULL;//    = 0x9A
  
M2=0x51D022F0946028C0

Шестнадцатеричные константы справа получены методом сдиг-редуцирование. Сдвиги выполняются независимо по каждому разряду.

Изоморфные отображения между представлениями полей

Представлением поля назовем поля сформированные с использованием двух основных вещей -- это нередуцируемый полином и генератор поля. Геренатором поля может быть любой примитивный элемент поля. Все числа кроме нуля можно получить методом возведения в степень генератора поля. Множество чисел в поле Галуа начинается с нуля b и считаются последовательно только в человеческом представлении. В нечеловеческом представлении можно установить однозначное соответствие между степенями некоторого примитивного элемента одного поля и примитивного элемента другого поля. В частности рассматриваем изоморфизм между полем GF(2^8)/p=0x1C3 -- "ГОСТ Streebog/Кузнечик" и полем GF(2^8)/p=0x11B -- AES. Когда говорим про изоморфное преобразование надо уточнять, какие именно примитивные элементы поля использованы для отображения. Отображений великое множество, примерно половина элементов поля может оказаться примитивными элементами, вариантов отображения много.

Нам нужна функция, которая определяет, является ли выбранный элемент поля примитивным. И способ поиска минимального примитивного элемента поля.

Кроме того, нам понадобится функция, которая находит решение матричного уравнения вида A*x=C. Поиск матрицы отображения - это решение восьми таких уравнений, для каждого столбца матрицы отображения.

Свойства изоморфизма (отображения представлений поля) -- линейность.
	map(a×b) = map(a)×map(b)
	map(a⊕b) = map(a)⊕map(b)

Это означает, что можно выполнить переход от одного поля в другое, выполнить расчет и вернуться обратно. Это значит, что мы можем перейти из поля Национальной криптографии 1С3 (ГОСТ) в поле иностранной криптографии 11B, использовать аппаратную функицию умножения и поиска обратного числа, затем отобразить результат расчета в поле национальной криптографии. Хочу заметить, что свойство линейности отображения позволяет выполнить эту операцию в два действия с использованием таблиц подстановки и векторной инструкции SHUFFLE. Отображения бывают разные. Представим, что отобразить можно в поле, где операций меньше или сложность операции становится меньше. Например существует отображение в композитные поля типа GF((2^4)^2).

Разные утверждения в конечном поле можно доказывать методом перебора всех элементов поля. Можно решать уравнения методом подбора решения. Вот и матрицы мы будем искать методом подбора. Разыскиваем такое Отображение для двух выбранных полей. Для каждого поля мы выбираем примитивный элемент, проверяем его примитивные свойства, находим матрицу отображения и проверяем, чтобы отображение работало для всех степеней k=0..255. Если отображение не работает, выбираем другой примитивный элемент.

Определение изоморфного отображения представлений поля GF(2^8)
	a - примитивный элемент поля с полиномом A(x)
	b - примитивный элемент поля с полиномом B(x)
	bk = M·ak
	ak = M-1bk
	M·M-1 = E

Алгоритм проверки элемента поля на примитивность состоит в том, что данный элемент является генератором, т.е. генерирует 255 элементов поля без повтора.

В качестве теста я использовал алгоритм генерации таблицы инверсии.

/* Алгоритм генерации таблицы инверсии 
 Poly - образующий полином поля GF(2^8), например 0x1C3
 g - генератор поля, например 0x02, 0x03
 Функция возвращает TRUE, если расчет дал 255 элементов поля.
 */
int initialize_inv(uint8_t inv[256], uint32_t g, uint32_t Poly)
{
	int count=0;
	uint8_t p = 1, q = 1;
	uint8_t g_inv = gf2p8_inverse(g, Poly);
	do {
		p = gf2p8_mul(p, g, Poly);
		q = gf2p8_mul(q, g_inv, Poly);
		inv[p] = q;
		if (++count>255) {
			break;
		}
	} while(p != 1);
	inv[0] = 0;
	return (count==255);
}

Среди прочих отображений хочу выделить главное - отображение, которое приводит степени генератора к диагональному виду.
1)Надо найти такие k_i: a^k_i = (1<<i), {01 02 04 08 10 20 40 80} в своем поле А.
2)Поместить в i-й столбец матрицы значение b^k_i.
Преобразование M переводит число a^k_i в число b^k_i в поле B. Числа вида (1<<i) испольщзуют только i-й столбец матрицы отображения M. Поэтому Матрица отображения в столбцах содержит сами значения b^k_i. Удобнее при этом соствлять матрицу по строкам, затем транспонировать к нормальному виду.

Привожу алгоритм составления матрицы отображения представлений поля.

/* Алгоритм составления матрицы отображения представлений поля
    PolyA - полином поля А,
    a   - генератор поля A,
    PolyB - полином поля B,
    b   - генератор поля B,
    Возвращает матрицу отображения
 */
uint64_t map_ab(uint8_t a, uint32_t PolyA, uint8_t b, uint32_t PplyB)
{
	uint64_t m=0;
	int i;
	for(i=0;i<8;i++){
		int k=1;
		uint8_t v=1, r=1;
		while (v != (1<<(i))) {
			v = gf2p8_mul(v, a, PolyA);
			r = gf2p8_mul(r, b, PplyB);
			k++;
		}
		m |= (uint64_t)r<<(8*(7-i));
	}
	// матрицу надо транспонировать
	return m_transpose(m);
}

Ниже привожу алгоритм подбора подходящего генератора поля для данного поля заданного полиномом и генератором {Poly1, g1} и искомого, заданного полиномом и начальным значением генератора поля {Poly2, g2}. В алгоритме вычисляется прямая (M) и обратная матрица (M^-1). Проверка выполняется по критерию, является ли одна матрица обратной для другой, M· M-1 == E. Идея построения такого алгоритма мне досталась с формуа криптографов [JeffaReid], остальные алгоритмы можно считать авторскими. Отладку алгоритма и всей методики выполнял по матрице отображения мажду полиномами 0x175 SM4 и 0x11B AES представленной в патенте[US9800406, S.Guerоn]. В работах S.Guerоn алгоритм поиска отображения не рассматривается, хотя в одной из публикаций дана ссылка на препринт, сам препринт недоступен. Также нигде не говориться о существовании нескольких вариантов отображения между представлениями полей. То что отображений несколько показано ниже, любое из полученных отображений будет работать.

/* Алгоритм подбора подходящего генератора поля */
uint8_t map_ab_test(uint8_t g1, uint32_t Poly1, uint8_t g2, uint32_t Poly2)
{
	int count=0;
	do {
		g2++;
		while (!(initialize_inv(inv, g2, Poly2))) g2++;
		map = map_ab(g1, Poly1, g2, Poly2);
		map1= map_ab(g2, Poly2, g1, Poly1);
		if (m_mul(map1, map)== E) {
        // Отображение найдено!!
        	break;
		}
	} while (1);
	return g2;
}

Ниже привожу результат работы алгоритма. Алгоритм находит все матрицы прямого и обратного отображения между представлениями поля. Всего нашлось по 8 шт таких матриц для каждого отображения. Построение выполнил для чертырех полиномов, которые меня заинтересовали. В качестве первого аргумента выбран минимальный примитивный элемент поля. Генератор второго поля подобран в алгоритме.

матрица для 1C3 => 11B "Kuznyechik"
 A    B   a  b           M                    M-1
1C3=>11B 02 30 M =5D0CE430CEE6BCD0 M-1 =C9248C8EB6BE7C4A
1C3=>11B 02 70 M =61D8CC543E9296A4 M-1 =359C60B0663A0EDA
1C3=>11B 02 77 M =2FA2EA44FA5AD66C M-1 =6332D8D6145ED06E
1C3=>11B 02 7A M =59A208A62EC29AF4 M-1 =61EC0A04B4F2D01C
1C3=>11B 02 98 M =ED406082D258646E M-1 =89F844381A0602F0
1C3=>11B 02 C1 M =5BD81880DC3CDA0A M-1 =494212C2C6360E08
1C3=>11B 02 C9 M =0340F81A7C8C1EBA M-1 =87864834BAD4025C
1C3=>11B 02 DC M =C90C4A9E5604C632 M-1 =195A202216CC7C46

матрица для 171 => 11B "Stribog"
171=>11B 02 0E M =49A24EE22C984CF0 M-1 =FB44BAF0CC5A0A1C
171=>11B 02 17 M =C30E560C5240D828 M-1 =6D0A141C3A9C2046
171=>11B 02 52 M =B1A27CD0765CD234 M-1 =F5481A5CBE24D86E
171=>11B 02 54 M =29903A0892D47ABC M-1 =E5126608F2EC44F0
171=>11B 02 A0 M =C154448014AEDCC6 M-1 =1B8C164A06F81208
171=>11B 02 B4 M =1590FECC3E8E8CE6 M-1 =9960C6DA5E32485C
171=>11B 02 F6 M =090EFAA096722E1A M-1 =6FD8B46E36428C4A
171=>11B 02 FD M =A7541EDA2602426A M-1 =CB20B646D48660DA

матрица для 1F5 => 11B "SM4"
1F5=>11B 02 23 M =C772D8A4A8EEE4B0 M-1 =ED166E76E6BA48DC
1F5=>11B 02 3E M =3D0EE232C2D63888 M-1 =0B664A2E7A14D8AE
1F5=>11B 02 65 M =0BFCBE30BCDAE684 M-1 =8D14F098CEC61270
1F5=>11B 02 69 M =8BFC9C12C00A4A54 M-1 =51B45C94BC666070
1F5=>11B 02 86 M =01DEF6D40840181E M-1 =011ADA10501620A2
1F5=>11B 02 8E M =110E9E4EE0589406 M-1 =A9C64682A8B40AAE
1F5=>11B 02 CE M =6572562A78CC1692 M-1 =43B61CA4EA1A44DC
1F5=>11B 02 D6 M =51DE2604863CEA62 M-1 =71BA0862FCB68CA2

матрица для 165 => 11B "BelT"
165=>11B 02 18 M =DD04D04E96781490 M-1 =1B92021C42FA84C2
165=>11B 02 48 M =CD6480F638C48E2C M-1 =FBE27CDAEC265804
165=>11B 02 57 M =979A3EC0E25C52B4 M-1 =99FAD04A86E23C34
165=>11B 02 5B M =5F127C6AD66C3684 M-1 =6F260EF0244C928E
165=>11B 02 A5 M =2704C658680E9CE6 M-1 =CB4C026E9C84FAB0
165=>11B 02 E7 M =D3120A1C4892567A M-1 =6D580E5C5A924C22
165=>11B 02 EB M =7B9AA05E944A32A2 M-1 =E584D046F83CE238
165=>11B 02 F5 M =BF647E082E5A06B2 M-1 =F53C7C08325826D6

матрица для 11D => 11B "Kalyna"
11D=>11B 02 03 M =FFAACC88F0A0C080 M-1 =FFAACC88F0A0C080
11D=>11B 02 05 M =CFB00A10BC602840 M-1 =DDE4F2E008A080AA
11D=>11B 02 11 M =5BD4D0B4F6487068 M-1 =D9B2068A4AA0AAE4
11D=>11B 02 1A M =DDEE9CA64E38FC18 M-1 =E12C36EE6EA0E4B2
11D=>11B 02 4C M =95D4EA8EEC0C2E2C M-1 =7BC0D4F446A078E8
11D=>11B 02 5F M =6FAAD692CAC49EE4 M-1 =2378BEF65CA0B22C
11D=>11B 02 E5 M =3BB06E74F85A567A M-1 =ADE85E3EDAA02C78
11D=>11B 02 FB M =57EED8E22A228202 M-1 =4F803A301CA0E8C0

Приведенные выше преобразования относятся к отображениям между представлениями, изоморфные. А как насчет возможности отобразить представление поля на себя?

Отображение представления поля на себя
1C3=>1C3 02 02 M =0102040810204080 M-1 =0102040810204080
1C3=>1C3 02 04 M =D1B0C26084C0D830 M-1 =0B24924A2AAAA282
1C3=>1C3 02 10 M =BD745818F2E80C44 M-1 =65388CCCC4460CA6
1C3=>1C3 02 1F M =A34EE6EA26B84054 M-1 =A34EE6EA26B84054
1C3=>1C3 02 96 M =91CA5AF8B214D89E M-1 =075E3CE41C48A21A
1C3=>1C3 02 A0 M =65388CCCC4460CA6 M-1 =BD745818F2E80C44
1C3=>1C3 02 C3 M =075E3CE41C48A21A M-1 =91CA5AF8B214D89E
1C3=>1C3 02 FD M =0B24924A2AAAA282 M-1 =D1B0C26084C0D830

Первое отображение, понятно - на себя (Диагональная матрица E), второе - дает квадраты чисел.. Это все квадраты и корни квадратные в поле 0x1С3: 02²=04, 04²=10, 10²=C3, C3²=1F, 1F²=96, 96²=A0, A0²=FD, FD²=02. Всего существует 8 таких отображений, по этой же причине существует по 8шт отображений в каждое представление поля.

Чего не удается получить аффинными преобразованиями:
Инверсия числа - найти обратное не получается с использованием только аффинных преобразований.

Пример 1. Линейные преобразования AES S-Box

Матрица аффинных преобразорваний AES S-Box состоит из матриц циклических сдвигов

A = E ^ (E<<56 ^ E>>8) ^ (E<<48 ^ E>>16) ^ (E<<40 ^ E>>24) ^ (E<<32 ^ E>>32);
где E - единичная диагональная матрица.

A =F1E3C78F1F3E7CF8₁₆ -- результат сложения матриц.

Обратная матрица аффинных преобразорваний AES InvS-Box
A-1= (E<<56 ^ E>>8) ^ (E<<40 ^ E>>24) ^ (E<<16 ^ E>>48);

A^-1=A44992254A942952₁₆ -- обратная матрица

Прямая и обратная Матрица AES [NIST FIPS 197]
   |1 1 1 1 1 0 0 0| =F8            |0 1 0 1 0 0 1 0| =52
   |0 1 1 1 1 1 0 0| =7C            |0 0 1 0 1 0 0 1| =29
   |0 0 1 1 1 1 1 0| =3E            |1 0 0 1 0 1 0 0| =94
A =|0 0 0 1 1 1 1 1| =1F    A^{-1} =|0 1 0 0 1 0 1 0| =4A
   |1 0 0 0 1 1 1 1| =8F            |0 0 1 0 0 1 0 1| =25
   |1 1 0 0 0 1 1 1| =C7            |1 0 0 1 0 0 1 0| =92
   |1 1 1 0 0 0 1 1| =E3            |0 1 0 0 1 0 0 1| =49
   |1 1 1 1 0 0 0 1| =F1            |1 0 1 0 0 1 0 0| =A4
   
C =(1 1 0 0 0 1 1 0) =63    A^{-1}С=(0 0 0 0 0 1 0 1) =05

Проверим, что синтезированная матрица дает ожидаемый результат...

b = affine_byte(0xF1E3C78F1F3E7CF8, gf2p8_inverse(a), 0x63);

a = gf2p8_inverse(affine_byte(0xA44992254A942952, b, 0x05));

Пример 2. Линейные преобразования SM4

A1 =A74F9E3D7AF4E9D3₁₆ -- матрица аффинных преобразований для S-Box SM4.

   |1 1 0 1 0 0 1 1| =D3
   |1 1 1 0 1 0 0 1| =E9
   |1 1 1 1 0 1 0 0| =F4
A1=|0 1 1 1 1 0 1 0| =7A
   |0 0 1 1 1 1 0 1| =3D
   |1 0 0 1 1 1 1 0| =9E
   |0 1 0 0 1 1 1 1| =4F
   |1 0 1 0 0 1 1 1| =A7

C1=(1 1 0 1 0 0 1 1) =D3

// функция генерации таблицы S-Box SM4
C1 = 0xD3;
SBox_SM4[i] = affine_byte(A1, Inv_SM4[affine_byte(A1, i, C1)], C1);

В этом примере Inv_SM4[256] - таблица инверсии по полиному 0х175, получена функцией initialize_inv().

Выражение, которое должно было получиться
s(x) = A2·Inv(A1·x ⊕ C1) ⊕ C2.

В моем случае матрица A2 получилась равной A1 и С2 равно С1. Вероятнее всего где-то не совпал порядок бит, у меня или в работе S.Gueron, но мое выражение для SBox оказалось проще. В примере 3. рассмотрим вопрос оторажения порядка следования бит.

Пример 3. Отражение и вращение матрицы

Есть множество алгоритмов, где используется отраженный порядок бит. В матричном представлении нам достаточно поменять строки матрицы местами, чтобы подстроиться под заданный порядок бит на выходе операции. Или надо менять столбцы местами, чтобы подстроится под заданный порядок бит на входе. Иногда это сложно представить сразу. Мне кажется проще это делать методом последовательного наложения матриц. Представим себе матрицу, которая меняет положение бит в векторе на обратное, назовем матрицу R=8040201008040201. В общем случае замес может быть более сложный, поэтому представляем себе матрицу замеса R и обратную матрицу которая возвращает биты на место R^-1. Есть несколько вариантов применения:

y = R·x -- меняет порядок следования бит.
y = R·A·x -- меняет порядок бит на выходе операции А.
y = A·R·x -- меняет порядок бит на входе операции А.
y = R-1·A·R·x -- меняет порядок на входе, на выходе возвращает к исходному.

   T=0x1122334455667788
    T             T*R            R*T           R*T*R
10001000 =88   00010001 =11   00010001 =11   10001000 =88
01110111 =77   11101110 =EE   00100010 =22   01000100 =44
01100110 =66   01100110 =66   00110011 =33   11001100 =CC
01010101 =55   10101010 =AA   01000100 =44   00100010 =22
01000100 =44   00100010 =22   01010101 =55   10101010 =AA
00110011 =33   11001100 =CC   01100110 =66   01100110 =66
00100010 =22   01000100 =44   01110111 =77   11101110 =EE
00010001 =11   10001000 =88   10001000 =88   00010001 =11

Для нашей матрицы R обратной операцией является тот же самый разворот R^-1=R. В примере видно, что матрица отражается по вертикали или горизонтали, последнее преобразование разворачивает матрицу на 180градусов.

Пример 4. Выполнение операций в изоморфном представлении поля

y = Inv(x, Poly1);
y =M-1·Inv(M·x , Poly2);

Предлагается проделать операцию инверсии и убедиться, что результат идентичен для нескольких представлений поля. Матрица M выполняет изоморфноего преобразование из представления с полиномом 0x1C3 в представление с полиномом 0x11B, операция инверсии выполняется в поле 0x11B. Также можно проверить работу с отображением в то же представление поля 0x1C3.

Для x=0xA5: Inv(0xA5, 0x1C3)==0x5B
Poly1 Poly2 g1  g2 
 1C3 =>1C3, 02, 1F, M =A34EE6EA26B84054 M-1 =A34EE6EA26B84054
 1C3 =>1C3, 02, C3, M =075E3CE41C48A21A M-1 =91CA5AF8B214D89E
 1C3 =>11B, 02, 30, M =5D0CE430CEE6BCD0 M-1 =C9248C8EB6BE7C4A
 1C3 =>11B, 02, DC, M =C90C4A9E5604C632 M-1 =195A202216CC7C46

У меня работает! Результат идентичный: 0x5B.

GF2p8 Представления конечных полей

Речь пойдет про математику, и приложение новых инструкций Intel GFNI для криптографии и оптимизации разных алгоритмов.

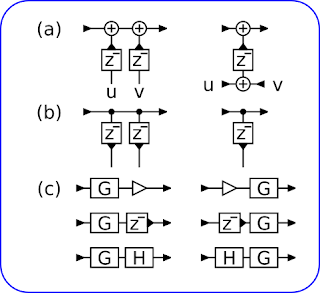
Во-первых, никто не понимает, как пользоваться инструкциями GF-NI - нечеловеческая математика. Расширение состоит из трех инструкций, которые расчитывают матричные операции над полиномами: M*x+C, M*x^-1+C и полиномиальное умножение с редуцированием A⊙B mod 0x11B. В систему команд введены инструкции для работы всего с одним полиномом (0x11B), в то время как этот полином используется мало в каких алгоритмах.

Первая операция M*x+C (аффинные преобразования gf2p8affine) не привязана никак к полиному(0x11B), можно сказать про полином вида x8+1, по которому выполняется редуцирование.

Операцию циклического сдвига A<<<n можно представить, как умножение и редуцирование по полиному x8+1. Запишется так: A×2ⁿ mod 0x101. Боже, откуда такое чувство, что меня никто не понимает?! Полиномиальное представление двоичных чисел - это просто термин такой, буквой x обозначается сдвиг на разряд. Вот что, например, написано про полиномиальное умножение в стандарте AES.. Rijndael S-box можно представить, как аффинное преобразование от обратного числа и записать в виде набора цикличекских сдвигов.

s = b ⊕ (b<<<1) ⊕ (b<<<2) ⊕ (b<<<3) ⊕ (b<<<4) ⊕ 6316

Это же утверждение записать через операцию полиномиального умножения (умнжения без переносов) и операцию редуцирования по полиному.

S = A×3110 mod 24710.

Это чтобы всех запутать сделано: числа даны в десятичном виде, операции в поле - умножение полиномиальное и редцирование по полиному x⁸+1.

Первое, что нашлось по теме использования инструкции - много циклических сдвигов можно представить, как аффинное преобразование [0x80.pl].

Из всего это следует, что подстановку AES S-box можно выполнить единственной инструкией gf2p8affineinv: S = A*inv(x)+C. Надо понять, как записать и протестировать эту возможность. Матрица преобразования записана в стандарте AES.

// Матрица аффинного преобразования, сдвиги: 0,1,2,3,4
|11111000|
|01111100|
|00111110|
|00011111|
|10001111|
|11000111|
|11100011|
|11110001|

// Матрица Обратного аффинного преобразования, сдвиги: 1,3,6
|01010010| 
|00101001|
|10010100|
|01001010|
|00100101|
|10010010|
|01001001|
|10100100|

Сдвиги в прямой матрице можно представить полиномом 7й степени (x7+x3+x2+x+1)=0xF1 сдвиги в обратной (x7+x5+x2)=0xA4. Для расчета обратного преобразования предлагается использовать утверждение (x7+x3+x2+x+1)^3 mod (x8+1)==(x7+x5+x2). Методом уножения на себя два раза из полинома 7й степени можно получить обратный ему полином.

Таким образом, утверждается, что имея полином A 7й степени, можно получить обратный ему полином B 7й степени, для которых выполняется условие A×B mod (x8+1) = 1. Не уверен, что это правило работает, но оставил.

// Нахождение обратного полинома 7й степени.
void inverse_af2(uint32_t poly)
{
	uint32_t mask = 0xFF;
	uint32_t p = poly & mask;
	uint32_t r;
	r = pmul(p, p);// умножение полиномиальное
	r = (r ^ (r>>8))& mask;// редуцирование
	r = pmul(r, p);// умножение полиномиальное
	r = (r ^ (r>>8))& mask;// редуцирование
	return r;
}

Навык поиска обратного значения нам понадобился, чтобы составлять прямые и обратные матрицы аффинных преобразований.

Обратный полином можно найти и методом подбора, перебрать все элементы поля, пока не найдется удовлетворяющий условию -- произведение на обратный элемент дает единицу.

// Операция умножения в поле GF(2^8) с полиномом Poly
uint32_t gf2p8_mul(uint32_t p, uint32_t i, uint32_t Poly){
    uint32_t r=0;
    while (i) {
        if (i&1)r^=p;
        if (p&0x80){
            p=(p<<1) ^ Poly;
        } else
            p=(p<<1);
        i>>=1;
    }
    return r;
}

Следующий инструмент разработки - составление таблиц преобразования, прямых и обратных. Тут надо вспомнить некоторое свойство. После g^(p-1) = g. Число g - генератор поля выбирается таким образом чтобы его степени проходили по всем элеементам - это, например, число 3. Методом уножения числа на 3 можно перебрать все элементы поля.

// Инициализация таблицы инверсии inv(x) == x-1
static void initialize_inv(uint8_t inv[256]) 
{
    uint8_t p = 1, q = 1;
    do {
        p = gf2p8_mul(p, 0x03, Poly);// умножить p на 3
        q = gf2p8_mul(q, 0xF6, Poly);// делить   q на 3
        inv[p] = q;
    } while p != 1);
    inv[0] = 0;
}

В цикле используется умножение на обратное число (0xF6), вместо деления на 3. Произведение чисел p и q единица, одно для другого на каждом цикле остается обратным числом. За счет выбора генератора, перебираются все числа, кроме нуля. В результате получаем таблицу обратных чисел.

Таблица обратных чисел для Poly=11B
 00 01 8D F6 CB 52 7B D1 E8 4F 29 C0 B0 E1 E5 C7
 74 B4 AA 4B 99 2B 60 5F 58 3F FD CC FF 40 EE B2
 3A 6E 5A F1 55 4D A8 C9 C1 0A 98 15 30 44 A2 C2
 2C 45 92 6C F3 39 66 42 F2 35 20 6F 77 BB 59 19
 1D FE 37 67 2D 31 F5 69 A7 64 AB 13 54 25 E9 09
 ED 5C 05 CA 4C 24 87 BF 18 3E 22 F0 51 EC 61 17
 16 5E AF D3 49 A6 36 43 F4 47 91 DF 33 93 21 3B
 79 B7 97 85 10 B5 BA 3C B6 70 D0 06 A1 FA 81 82
 83 7E 7F 80 96 73 BE 56 9B 9E 95 D9 F7 02 B9 A4
 DE 6A 32 6D D8 8A 84 72 2A 14 9F 88 F9 DC 89 9A
 FB 7C 2E C3 8F B8 65 48 26 C8 12 4A CE E7 D2 62
 0C E0 1F EF 11 75 78 71 A5 8E 76 3D BD BC 86 57
 0B 28 2F A3 DA D4 E4 0F A9 27 53 04 1B FC AC E6
 7A 07 AE 63 C5 DB E2 EA 94 8B C4 D5 9D F8 90 6B
 B1 0D D6 EB C6 0E CF AD 08 4E D7 E3 5D 50 1E B3
 5B 23 38 34 68 46 03 8C DD 9C 7D A0 CD 1A 41 1C

Заметим, что аналогичным образом можно составить таблицу экспоненты и логарифма числа, в качестве генератора используется число 2. Т.е. табличное представление умножения и инверсии через экспонирование и логарифирование чисел, с отображением на конечное поле 255 с обычной модульной арифметикой -- это нас не пугает, потому что традиционно используется в расчетах кодов Рида-Соломона. Интересно, можно ли аффинными преобразованиями получить экспоненту или логарифм числа, чтобы заменить таблицы на аффинные преобразования?

Вернемся к генерации таблиц.

S = A×inv(x)⊕C = AF(inv[x])⊕ 6316

Всего существует 30шт нередуцируемых полиномов восьмого порядка, которые можно использовать для построения полей GF(2^8). Утверждается, что все поля образованные нередуцируемыми полиномами 8-ого порядка изоморфны, т.е. имеют однозначное отображение одного множества чисел на другое множество. Это можно не доказывать, и так очевидное утверждение.

Другое утверждение -- представления полей GF(2^8) с разными полиномами можно отображать используя аффинные преобразования с матрицей 8x8 бит. Вот только как эти матрицы получать? Погуглить в интернете?! Нашел работы 2019-2021 года по разработке новых алгоритмов для пост-квантовой криптографии, нашел оптимизации таблиц подстановок типа S-box на основе таких преобразований. От Intel традиционно, внедрение новых инструкций Intel для криптографии продвигает Shay Gueron и группа товарищей, по его работам, патентам с его участием и статьям можно проследить развитие направления.

[US9800406] US Патент описывет преобразование представления GF(2^8) для вычисления S-Box китайского национального алгоритма блочного шифра SM4. Образующий поле AES полином x8 + x4 + x3 + x + 1=0x11B, в SM4 используется образующий полином x8 + x7 + x6 + x5 + x4 + x2 + 1=0x1F5. Преобразования Sbox записывается следующим образом.

SBoxSM4(x) = A2*inv(A1*x⊕C1)⊕C2
SBoxAES(x) = A*inv(x) + 6316

Матрицы SM4
   |1 0 1 0 0 1 1 1|    |1 1 0 0 1 0 1 1|
   |0 1 0 0 1 1 1 1|    |1 0 0 1 0 1 1 1|
A1=|1 0 0 1 1 1 1 0| A2=|0 0 1 0 1 1 1 1|
   |0 0 1 1 1 1 0 1|    |0 1 0 1 1 1 1 0|
   |0 1 1 1 1 0 1 0|    |1 0 1 1 1 1 0 0|
   |1 1 1 1 0 1 0 0|    |0 1 1 1 1 0 0 1|
   |1 1 1 0 1 0 0 1|    |1 1 1 1 0 0 1 0|
   |1 1 0 1 0 0 1 1|    |1 1 1 0 0 1 0 1|
   
C1=(1 1 0 0 1 0 1 1)TC2=(1 1 0 1 0 0 1 1)T

Матрица AES [NIST FIPS 197]
   |1 0 0 0 1 1 1 1|
   |1 1 0 0 0 1 1 1|
   |1 1 1 0 0 0 1 1|
A =|1 1 1 1 0 0 0 1|
   |1 1 1 1 1 0 0 0|
   |0 1 1 1 1 1 0 0|
   |0 0 1 1 1 1 1 0|
   |0 0 0 1 1 1 1 1|

C =(1 1 0 0 0 1 1 0)T

Патент представил матрицу преобразования элементов из поля SM4(0x1F5) в поле AES(0x11B)

Матрица отображения
  |0 1 1 0 0 0 1 0|
  |1 1 1 0 1 0 1 0|
  |0 0 1 1 1 1 0 0|
M=|1 0 0 0 0 1 1 0|
  |0 0 0 0 0 1 0 0|
  |0 0 1 0 0 1 1 0|
  |1 1 0 1 1 1 1 0|
  |0 1 0 1 0 0 0 1|

Отображение из SM4 в AES можно описать выражением

y = M*(A1*x⊕C1)

Обратное отображение из AES в SM4

s = A2*(M-1*A-1*u)⊕C2

Матрицы 8x8 можно перемножать между собой и сокращать выражения.

Матрицы отображения
     |01010010|             |11001011|
     |10111100|             |10011010|
     |00101101|             |00001010|
M*A1=|00000010|, A2*M-1*A-1=|10110100|
     |10011110|             |11000111|
     |00100101|             |10101100|
     |10101100|             |10000111|
     |00110100|             |01001110|

M*C1=0x65               C2 =0xD3

Такие же преобразования можно совершать в любом поле. Всего насчитывается 30 нередуцируемых полиномов пригодных для подобных преобразований.

Для разработки необходимы методы: 1) Поиск матриц M для перехода между представлениями, 2) Декомпозиция S-Box 3) перемножение матриц, поиск обратных матриц, произведение матрицы на вектор - линейная алгебра. Из своего образования вспоминаю LU-разложение матриц, и свойства линейности матриц, которое позволяет представлять аффинные преобразования в виде перестановок, т.е снизить разрядность операции. Надо вспоминать линейную алгебру! Довольно много разных алгоритмов используют различные полиномы. Эти инструкции позволяют существенно ускуорить их работу, но пока нет опыта использования и надо затратить усилия на освоение математики и разработку алгоритмов синтеза таблиц.

Ниже привожу таблицу нередуцируемых полиномов..

Таблица нередуцируемых полиномов (30 шт):
x^8 + x^7 + x^5 + x^4 + 1
x^8 + x^6 + x^5 + x^4 + 1
x^8 + x^7 + x^5 + x^3 + 1
x^8 + x^6 + x^5 + x^3 + 1
x^8 + x^5 + x^4 + x^3 + 1
x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + 1
x^8 + x^6 + x^5 + x^2 + 1
x^8 + x^7 + x^6 + x^5 + x^4 + x^2 + 1
x^8 + x^7 + x^3 + x^2 + 1
x^8 + x^6 + x^3 + x^2 + 1
x^8 + x^5 + x^3 + x^2 + 1
x^8 + x^4 + x^3 + x^2 + 1
x^8 + x^7 + x^6 + x^4 + x^3 + x^2 + 1
x^8 + x^7 + x^5 + x^4 + x^3 + x^2 + 1
x^8 + x^7 + x^6 + x + 1
x^8 + x^7 + x^5 + x + 1
x^8 + x^6 + x^5 + x + 1
x^8 + x^7 + x^6 + x^5 + x^4 + x + 1
x^8 + x^7 + x^3 + x + 1
x^8 + x^5 + x^3 + x + 1
x^8 + x^4 + x^3 + x + 1 - AES
x^8 + x^6 + x^5 + x^4 + x^3 + x + 1
x^8 + x^7 + x^2 + x + 1
x^8 + x^7 + x^6 + x^5 + x^2 + x + 1
x^8 + x^7 + x^6 + x^4 + x^2 + x + 1
x^8 + x^6 + x^5 + x^4 + x^2 + x + 1
x^8 + x^7 + x^6 + x^3 + x^2 + x + 1
x^8 + x^7 + x^4 + x^3 + x^2 + x + 1
x^8 + x^6 + x^4 + x^3 + x^2 + x + 1
x^8 + x^5 + x^4 + x^3 + x^2 + x + 1

Следующая статья по теме - закрепление. Материала много для одного сообщения, но надо дополнить.

[S.Gueron et al. Speed up over the Rainbow] "All the representations of GF(2^8) are isomorphic. Therefore, it is possible to pass from one representation to another by means of multiplying by an 8 ×8-bit matrix"

OpenPGP цифровая подпись файлов

Начал разбираться с проверкой цифровых подписей в документах налоговой, не понравилось, не пошло.. Переключился на цифровую подпись файлов в линуксе, GnuPG.

Меня почему-то беспокоит, что подпись есть, а как она формируется я не знаю, еще не знаю откуда она взялась и кто ее контролирует. Вдруг мне система начинает задавать вопросы: доверять этому отпечатку подписи или нет?! Стал разбираться.

Открыл стандарт [RFC 4880], открыл проект gpg/GnuPG, посмотрел что пишет Вернер Кох в драфте очередной переработки на стандарт OpenPGP [RFC 4880]. Написал свой собственный парсер цифровой подписи. Хочу поделиться мыслями и впечатлениями.

Кому-то лень развивать формат OpenPGP

Мне хотелось увидеть цифровую подпись Гост, потому что Митя занимается внедрением цивровой подписи ГОСТ в библиотеку libgcrypt, на базе которой работает GnuPG.

Каково было обнаружить, что ничего нового в OpenPGP не поддерживается. В основном это упирается в стандартизацию и документацию. Библиотека libGCrypt поддерживает множество разных подписей и дайджестов, включая Китайские SM и Российские ГОСТ. НО все уперлось в то, что в GnuPG не описаны идентификаторы этих дайджестов подписей.

Пока писал программку не оставляет чувство, что это зря забытая технология. Нет, но почему забытая?! PGP ключи используются для подписи программ в множестве дистрибутивов Linux, в MSYS2. Однако, тут в чем беда, я хочу криптографию на бублике и хеши ГОСТ, а мне предлагают RSA и SHA256. Я не хочу, чтобы GnuPG умер, надо в него для долгой жизни добавить еще идентификаторов алгоритмов.

Инфраструктура OpenPGP

На чем держится все? На доверии, самоподписанные ключи разработчиков попадают в дистрибутив и распространяются с обновлением дистрибутива. Кроме того есть возможность находить сервера для проверки сертификатов через DNS записи зоны - но это скорее корпоративный стиль, вряд ли возможно поддержать такой способ в Linux. Нужен децентрализованный способ распространения и хранения ключей. Еще одна возможность - это списки доверенных серверов хранения ключей, которые можно поместить в сертификацию.

Сертификация

Я занимаюсь реверс инжинирингом. Не претендую на истину. Мое мнение - собственное, основано на том, что я вижу в коде. А вижу я свободно компануемую форму, которая называется "сертификация". В отличие от сертификатов x509, сертифицируется последовательность записией. Сертифицируется цифровой подписью. Кодирование очень простое, не сильно структурированное. Такое кодирование можно поддержать в микронтроллере с малым объемом памяти. Ничего лишнего: публичный ключ, идентификатор подписи, и подпись. Лаконично. Моя реализация, которая умеет разбирать формат и проверять сертификацию и присоедиенные подписи (detached-sign) укладывается в 800 строк кода - вся утлита такого размера. При этом, со второй попытки могу написать реализацию раза в три короче, если выкинуть вербозность. Я увидел, что формат хорошо приспоосблен для общения между децентрализованными узлами: не текстовый, не сложный, можно построить что-то типа блок-чейна. Вторая особенность имеет возможность меняться без перевыпуска ключей, т.е. если узел в сети решил, что доверяет новому серверу ключей, то для этого не надо перевыпускать сертификат. Почему, потому что ключ идентифицируется по отпечатку, отпечаток выполняется от открытого ключа, только от самого ключа, даже не от имени владельца. Уупс. А что, можно переименовать владельца ключа без перевыпуска? ДА. Я смотрю формат. Вижу, что ключ идентифируется отпечатком, по отпечатку я ищу ключ в связке или на сервере ключей. Файл подписи содержит имя владельца и разные реквизиты, которые подписаны и подпись сходится, сертификация сходится - подмена состоялась, можно сказать владелец подписал. Тоже относится и к дате ключа и сроку действия. Поля подписаны, но не ясно как им доверять. Надо читать мануал...

Сертификация множества устройств для совместной работы

Я вообще-то представляю себе множество ботов, которым надо выстраивать общение между собой. Когда думаю про ботов, думаю про криптографию, блок-чейн, цепочки доверия. PGP очень даже подходит. Устройство регистрируется со своим сертификатом самоподписанным, со своим идентификатором, рождается с несколькими ключами, и использует их для интеграции в сообществе. Нужен ключевой сервер (Who has, Who Is,.. ) и алгоритмы привязки и миграции устройства между серверами на основе доверия и подписи. [GNU Privacy Handbook] -- досуг настал, пошел изучать концептуальные вещи, как реализовать общение между ботами, как выстраивать цепочки доверия и как менять принадлежность узла ключевому серверу, как переименовать и все такое, без смены ключа.

Цифровая подпись файлов (Detached-sign)

Ниже привожу вывод моей программы по разбору сертификатов для сочетания алгоритмов RSA и SHA256, которые GPG использует по умолчанию. Формат PGP состоит из склеенных в определенной последовательности пакетов PGP. В последовательности встречаются цифровые подписи, которые сертифицируют предыдущие пакеты по правилам прописанным в стандарте [RFC4880].

Для проверки подписи файла понадобится сертификат открытого ключа. Сертификат импортируется в программу из GPG. Аналогично можно импортировать закрытый ключ и передать в другую программу или на другой компьютер. Подписываются три пакета: имя владельца, открытый ключ и субпакеты сертификации. Кстати, закрытая часть ключа не подписывается, она сама себе попдись от открытого ключа, можно проверить соответствие закрытого ключа и отокрытого математически.

## Пример. Импорт и Сертфикация закрытого ключа
$ ./mypgp -v --import=secret_key.pgp
-- PGP format --
type 5: 'Secret-Key Packet', Format v4, length=1414
        Created: 2021-06-03 15:03:04
        Key Alg: (1) RSA
RSA modulus n:
 E2 F0 68 AF . . . E5 B2 85 C1
RSA public exp:
 01 00 01
-- PGP format --
type 13: 'User ID Packet', length=52
        User ID: Anatoly Georgievskii <anatoly.georgievski@gmail.com>
-- PGP format --
type 2: 'Signature Packet', Format v4, length=468
-- version 4
-- sign type(19) Positive certification of a User ID and Public-Key packet
-- pkey alg (1) RSA
-- hash alg (8) SHA256
-- hash subpacket len 62-- Хешируемые записи
 -- 'Issuer fingerprint' subpacket(33), len=22
        Fingerprint: -- расчитан от открытого ключа.
 04 750E . . . 05C1B196BBF9564E
 -- 'Signature Creation Time' subpacket(2), len=5
        Creation  : 2021-06-03 15:03:04
 -- 'Key Flags' subpacket(27), len=2
 -- 'Key Expiration Time' subpacket(9), len=5
 -- 'Preferred Symmetric Algorithms' subpacket(11), len=5
        Algorithms: AES256 AES192 AES128 TDES
 -- 'Preferred Hash Algorithms' subpacket(21), len=6
        Algorithms: SHA512 SHA384 SHA256 SHA224 SHA1
 -- 'Preferred Compression Algorithms' subpacket(22), len=4
        Algorithms: ZLIB BZip2 ZIP
 -- 'Features' subpacket(30), len=2
 -- 'Key Server Preferences' subpacket(23), len=2
digest:-- Хеш от записей: UserId|PublicKey|hash_subpackets
 B5D1 9DFF . . . 1CA0 CFEE
-- data subpacket len 10
 -- 'Issuer' subpacket(16), len=9
 -- issuer Key Id: 05C1B196BBF9564E 
 -- 8 байт в конце Fingerprint образуют уникальный идентификатор ключа
-- hash octets.. B5D1 -- 2 байта Хеша вписаны в формат
-- sign len 3070 bits:
 28 02 10 26 . . . 3B 20 F8 5C
-- Сертификация пройдена! Выполнена проверка подписи секретного ключа.

Cосуществование форматов OpenPGP и CMS

Есть предложение! Хочется установить соотвествие между сертифкацией OpenPGP и (detached) цифровыми подписями в формате CMS. Возможно ли использовать ключи и сертификаты x509 для генерации и проверки цифровой подписи PGP?

Это два действия.
1) Экспорт открытого ключа из x509 в PGP формате, при этом надо договориться об использовании и соответствии полей сертификата x509 и субпакетов PGP.
2) Генерация цифровой подписи detached-sign в формате PGP.

Цепочки доверия

Доверие сертификации - одноходовое. Если подпись авторитетная, то доверие есть. Система импортирует ключ, и оценивает авторитетность подписи по цепочке до самоподписанного доверенного сертификата. Доверенные сертификаты (ключи и атрибуты ключей) живут в связке (keyring). Связка ключей должна вызывать доверие.

Для примера нужна модель. Каждая сущность способная порождать файлы должна обладать возможностью сертификации. Мы говорим об операционной системе, которая порождает данные, сервисной программе, учетной записе пользователя. Данные можно порождать лично, или делегировать эту способность боту. Мы говорим о файловой системе, в которой необходимо хранить подписи и историю позволяющую выполнить проверку цепочки доверия. Допустим я беру всю файловую систему целиком без пользователя и без компьютера. Целостность нарушена, но может быть проверена и востановлена. Целостность подтверждается цепочками сертификации файлов. Все чего мы при этом лишились - это закрытого ключа. Структура файловой системы должна поддаваться анализу. Еще лучше, если анализ целостности позволяет выстраивать распределенную файловую систему. Например, представляем себе вместо установки операционной системы(вместо копирования файлов), копирование идентификаторов и сертификацию дистрибутива и серверов. Я пытаюсь запустить программу, которой нет на моем компьютере, но ее можно найти по идентификатору, по имени, с учетом сертификации в дистрибутиве. Каждый файл имеет происхождение, авторство. Каждое изменение файла или его части имеет сертификацию. . . . {дописать}

Векторное воплощение блочного шифра ChaCha20

Блочный шифр ChaCha - это просто[RFC 8439]. На решение задачи, как векторизовать алгоритм ушло полдня. Обратил внимание, как выглядит алгоритм в [libGCrypt]. Уныло.
Алгоритм ChaCha20 строится на примитивах QUARTERROUND.

// The ChaCha Quarter Round: QUARTERROUND(a,b,c,d)
      a += b; d ^= a; d <<<= 16;
      c += d; b ^= c; b <<<= 12;
      a += b; d ^= a; d <<<= 8;
      c += d; b ^= c; b <<<= 7;

-- сложения, исключающее или и циклические сдвиги. Таких раундов по матрице uint32х4х4 получается 8 в кажом цикле и всего 10 циклов.

// Тело цикла ChaCha
      QUARTERROUND(0, 4,  8, 12)
      QUARTERROUND(1, 5,  9, 13)
      QUARTERROUND(2, 6, 10, 14)
      QUARTERROUND(3, 7, 11, 15)
      QUARTERROUND(0, 5, 10, 15)
      QUARTERROUND(1, 6, 11, 12)
      QUARTERROUND(2, 7,  8, 13)
      QUARTERROUND(3, 4,  9, 14)

Вот так выглядит тело цикла, индексы в скобках - индексы массива состояния, всего 16 переменных. Не сложно заметить, каждая переменная участвует только в двух из восьми раундах. Присмотрелся -- первые четыре раунда могут выполняться параллельно и вторые четыре раунда могут выполнятся параллельно.

// Тело цикла ChaCha - векторизация по uint32х4 128 бит.
		a += b; d ^= a; d = ROL(d,16);
		c += d; b ^= c; b = ROL(b,12);
		a += b; d ^= a; d = ROL(d, 8);
		c += d; b ^= c; b = ROL(b, 7);
		b = SHUFFLE(b, 1, 2, 3, 0);
		c = SHUFFLE(c, 2, 3, 0, 1);
		d = SHUFFLE(d, 3, 0, 1, 2);
		a += b; d ^= a; d = ROL(d,16);
		c += d; b ^= c; b = ROL(b,12);
		a += b; d ^= a; d = ROL(d, 8);
		c += d; b ^= c; b = ROL(b, 7);
		b = SHUFFLE(b, 3, 0, 1, 2);
		c = SHUFFLE(c, 2, 3, 0, 1);
		d = SHUFFLE(d, 1, 2, 3, 0);

Вот так работает! Все операции - векторные, ROL - циклический сдвиг, SHUFFLE - перестановка слов.

Между строк написано, что ChaCha20 сделал по мотивам Salsa20. Структура та же - 8 раундов и 10 циклов.

// Тело цикла Salsa20 - векторизация по uint32х4 128 бит.
		// замена столбцов x3<=>x1
		x1 = SHUFFLE(x1, 1, 2, 3, 0);
		x2 = SHUFFLE(x2, 2, 3, 0, 1);
		x3 = SHUFFLE(x3, 3, 0, 1, 2); 
		x1 ^= ROL(x0 + x3, 7);
		x2 ^= ROL(x1 + x0, 9);
		x3 ^= ROL(x2 + x1,13);
		x0 ^= ROL(x3 + x2,18);
		// замена столбцов x3<=>x1
		x3 = SHUFFLE(x3, 1, 2, 3, 0);
		x2 = SHUFFLE(x2, 2, 3, 0, 1);
		x1 = SHUFFLE(x1, 3, 0, 1, 2);
		x3 ^= ROL(x0 + x1, 7);
		x2 ^= ROL(x3 + x0, 9);
		x1 ^= ROL(x2 + x3,13);
		x0 ^= ROL(x1 + x2,18);

Также как и в предыдущем случае, в переменных состояния {x0,x1,x2,x3} живут столбцы матрицы uint32х4x4. Для подготовки данных к такому алгоритму матрицу состояния пришлось транспонировать.

Производительность

Получил результат по производительности. Применил хитрость при измерении скорости. Загрузил состояние в кеш, и загрузил код в кеш, методом запустить дважды. Получилась производительность по алгоритмам примерно равная на уровне 80 тактов на 512 байт, 10 циклов для каждого алгоритма. Измерял на Intel Core-i3 Gen10.

Функции GHASH и POLYVAL в алгоритмах шифрования GCM и GCM-SIV

Придумал более эффективную реализацию функции умножения в поле GF128, на которой строится фукнция POLYVAL и GHASH. Делюсь..
Записал с использованием макро определений инструкций.

// Алгоритм умножения на инструкциях умжножения без переноса (PCLMUL).
__m128i gmul128r(__m128i a, const __m128i b)
{
    const __m128i  poly = _mm_setr_epi32(0x1,0,0,0xc2000000);
    __m128i  M,L,H;
    L = _mm_clmulepi64_si128(a, b, 0x00);
    M = _mm_clmulepi64_si128(a, b, 0x01);
    M^= _mm_clmulepi64_si128(a, b, 0x10);
    H = _mm_clmulepi64_si128(a, b, 0x11);
// редуцирование poly = 1.C2...01
    M^= _mm_shuffle_epi32(L, 78);
    M^= _mm_clmulepi64_si128(L, poly, 0x10);
// редуцирование 
    H^= _mm_shuffle_epi32(M, 78);
    H^= _mm_clmulepi64_si128(M, poly, 0x10);
    return H;
}

// Функция расчета кода аутентификации
__m128i POLYVAL(__m128i y, __m128i h, const uint8_t *data, int len)
{
    __m128i x;
    int i=0;
    int blocks = len>>4;
    for (i=0; i<blocks; i++){
        __builtin_memcpy(&x, data, 16); data+=16;
        y = gmul128r((y^x), h);
    }
    if (len & 0xF){
        x ^= x;
        __builtin_memcpy(&x, data, len&0xF);
        y = gmul128r((y^x), h);
    }
    return y;
}

// Функция расчета кода аутентификации
__m128i GHASH(__m128i y, __m128i h, const uint8_t *data, int len)
{
    int i=0;
    __m128i x;
    h = SLM128(h);// -- сдвиг с редуцированием, можно вынести из функции
    int blocks = len>>4;
    for (i=0; i<blocks; i++){
        __builtin_memcpy(&x, data, 16); data+=16;
        y = gmul128r((y^x), h);
    }
    if (len &0xF){
        x ^= x;
        __builtin_memcpy((uint8_t*)&x +(16-(len&0xF)), data, len&0xF);
        y = gmul128r((y^x), h);
    }
    return y;
}

Тут достижение в оптимизации фукнции редуцирования. Редуцирование выполняется по промежуточному значению M. Этот алгоритм меньше на три векторных инструкции, чем референсный [RFC8452]. Чтобы убедиться, надо лезть на github и сравнивать реализации[AES-GCM-SIV].

• [RFC 8452] AES-GCM-SIV, Gueron, et al., April 2019
• [AES-GCM-SIV] https://github.com/Shay-Gueron/AES-GCM-SIV
• [1] Enabling High-Performance Galois-Counter-Mode on Intel® Architecture Processors, 2012
• [2] Optimized Galois-Counter-Mode Implementation on Intel® Architecture Processors, 2010
• [3] Intel® Carry-Less Multiplication Instruction and its Usage for Computing the GCM Mode, 2009-2014

Алгоритм блочного шифра "Кузнечик"

Занимался оптимизацией алгоритма шифрования Кузнечик [ГОСТ Р 34.12-2015]. Последние действия могу объяснить, а откуда получены промежуточные, забываю. Надо зафиксировать знание. Чтобы восстановить логику, пишу статью. Цель статьи -- показать, как можно оптимизировать алгоритмы в конечном поле.

Цикл алгоритма состоит из трех преобразований (LSX): наложение колюча(X), табличная подстановка(S) и некоторые линейные действия в конечном поле GF(2^8) с полиномом 0x1С3.

Преобразование L состоит из множества умножений и сложений в конечном поле. Операцию L можно исключить и сделать табличной. А наоборот, нельзя ли вычислить L честно и в тоже время быстро?

L состоит из 16 циклов R замешивания и умножения. В результате можно написать произведение матрицы коэффициентов (LM) 16х16 элементов на вектор из 16 элементов: LM*(a) -- линейная алгебра в поле GF. Если в нашем распоряжении есть векторная инструкция умножения в конечном поле, то задача может быть решена.

В архитектуре ARM Neon есть инструкция полиномиального векторного умножения (vpmull_p8), которая позволяет выполнить 8 умножений параллельно, результат - вектор 128 бит состоящий из 8 произведений выполненных без переносов(полиномиальных). Чтобы вернуть результат умножения в поле, надо выполнить операцию редуцирования. Операция матричного умножения в поле GF(2^8)

// Операция  матричного умножения в поле GF(2^8)
// редуцирование вынесено из цикла
#include <arm_neon.h>
poly16x8_t v0 = {0};
poly16x8_t v1 = {0};
int i;
for(i=0; i<16; i++) {
    // размножаем значение на все элементы
    poly8x8_t a8 = (poly8x8_t)vdup_n_u8(sbox[a[i]]);
    // загружаем столбцы матрицы коэффициентов
    poly8x16_t p8 = LMT[i];
    // умножаем младшую часть вектора poly8x8
    v0 ^= vmull_p8(a8, vget_low_p8 (p8));
    // умножаем старшую часть вектора poly8x8
    v1 ^= vmull_p8(a8, vget_high_p8(p8));
}

В результате вектор {v0,v1} содержит результат матричного умножения, 16 элементов по 16 бит в двух векторных регистрах, который далее следует редуцировать до 8 бит, чтобы вернуть в поле GF(2^8).

Редуцирование выполняется по методу Баретта. В алгоритме редуцирования используется обратное число - константа баретта (0x1B5) и сам полином (0x1С3).

Редуцирование по Баретту напоминает остаток от деления.
q = a/P = a*B
r = a - q*P

В нашем случае нужно заменить операции на соответствующие операции в поле GF

Алгоритм №__. Редуцирование по Баретту B=0x1B5, P=0x1C3.
На Входе: [a1:a0]
    [q1:q0] := a1 ⊙ B -- операция умножения
    [r1:r0] := [a1:a0] ⊕ q1 ⊙ P
На выходе: r0

// редуцирование вынесли из цикла
    poly8x8_t t0;
	poly16x8_t t;
	const poly8x8_t B5 = vdup_n_p8(0xB5);
	const poly8x8_t C3 = vdup_n_p8(0xC3);
    // сдвиг вправо элементов вектора 16 бит на 8 бит с заужением
    t0 = (poly8x8_t) vshrn_n_u16((uint16x8_t)v0, 8);
    t  = vmull_p8(t0, B5);// 
    t0^= (poly8x8_t) vshrn_n_u16((uint16x8_t)t, 8);
    v0^= vmull_p8(t0, C3);// v0 := v0 - t0*P

Операция редуцирования выполняется над каждым элементом вектора v0 и v1. Результат - вектор poly16x8_t. Операция выполняется над вектором v1 - старшая часть вектора 16х16. Финально необходимо преобразовать вектор обратно к разрядности poly8x16_t

Аналогичный алгоритм может быть построен на операции умножения без переносов на платформе Intel, с использованием инструкции PCLMUL

//Матричное умножение в поле GF
    for(i=0;i<16;i+=1){
        a16[0] = sbox[a[i]];
        poly64x2_t L = (poly64x2_t)UNPACKLBW128((int8x16_t)LMT[i], Z);
        poly64x2_t H = (poly64x2_t)UNPACKHBW128((int8x16_t)LMT[i], Z);
        v0 ^= CL_MUL128(a16, L, 0x00);
        v1 ^= CL_MUL128(a16, L, 0x10);
        v2 ^= CL_MUL128(a16, H, 0x00);
        v3 ^= CL_MUL128(a16, H, 0x10);
    }

Привожу табличный алгоритм, чтобы было с чем сравнивать

//Векторное воплощение операции LSX
uint8x16_t LSX(uint8x16_t a, uint8x16_t K)
{
    poly64x2_t r0={0};
    poly64x2_t r1={0};
    int i;
    poly64x2_t bb= (poly64x2_t)(a ^ K);
    uint64_t b0 = bb[0];
    uint64_t b1 = bb[1];
#pragma GCC unroll 8
    for(i=0;i<8;i++) {
        uint64_t aa = a[i];
        r0 ^= LS[i  ][(b0>>(i*8))&0xFF];
        r1 ^= LS[i+8][(b1>>(i*8))&0xFF];
    }
    return (uint8x16_t)(r0 ^ r1);
}

Результат практический: удалось получить производительность на Intel Core (10th Gen) до 20 тактов на байт при шифровании MGM. В то время, как производительность табличного метода - в три раза выше. Теоретически можно пытаться увеличить производительность алгоритма за счет использования векторных инструкций VPCLMUL с разрядностью 256 и 512 бит. На платформе Arm Neon ожидаю сравнимую производительность с табличным методом, поскольку в цикле используется меньше инструкций. Данных по производительности на ARM пока нет.

Подведем итог. Результат отрицательный по быстродействию. Но, как мне кажется, заслуживает внимания. Алгоритм можно использовать в тех случаях, когда нужно минимизировать таблицы -- в микроконтроллерах.

Графика машинная

Охватить всю тему - писать книгу. Охватим в статье только линии и способ синтеза алгоритмов. Как для графического дисплея нарисовать линию. Прежде всего понадобится теория разработки алгоритмов для графики. Графика может быть полутоновая или черно-белая, но в обоих случаях пиксельная. Т.е. нам предстоит разработать алгоритмы для хождения по клеточкам.

$y(x)\; =\; (y2-y1)/(x2-x1)*(x-x1)\; +\; y1$

Представляем это уравнение, как функцию ошибки. В начальной точке y(x=x1) = y1, ошибка - отклонение от линии по Eps(x=x1) = 0. Отклонение накапливается с каждым шагом вдоль оси Х.

$Eps(x+1)\; :=\; Eps(x)\; +\; (y(x+1)\; -\; y(x))$
$Eps(x+1)\; :=\; Eps(x)\; +\; (y2-y1)/(x2-x1)$

На каждом шаге вдоль оси X надо прибавлять дробь. Если ошибка становится больше Eps>=0.5, то прибавляем, делаем шаг вдоль оси Y. На каждом шаге мы стремимся уменьшить ошибку, выполняем округление к ближайщему целому числу. Надо понимать, что мы вместо вещественных чисел работаем с дробными. С нормальными дробями, вещественные числа представляем в виде A/D = Q(R/D), где Q - целая часть от деления, R- остаток от деления, D- делитель.

X ++;
Y += Q;
Eps += R/D;
if (Eps >= 0.5) {
    Eps -= 1.0;
    Y ++;
}

На каждом шаге алгоритма мы компенсируем ошибку округления при делении. Точность попадания в конечную точку абсолютная. В конечной точке ошибка (Eps) - ноль. Вещественные числа не точны, там всегда происходит потеря точности, при работе с дробями - не теряется.

От вещественных чисел можно перейти к целым, домножив Eps на 2D

X ++;
Y += Q;
Eps += 2*R;
if (Eps >= D) {
    Eps -= 2*D;
    Y ++;
}

До меня этот алгоритм предложил Бразенхейм. Однако, простое человеческое осмысление способа синтезирования подобных алгоритмов я подсмотрел в своей голове.

Парабола

$y(x)\; =\; A*x^2\; +\; B*x\; +\; C$
$Eps(x+1)\; :=\; Eps(x)\; +\; 2A*x\; +\; 1\; +\; B$

x ++;
Eps += 2A*x + (1 + B);
if (Eps >= 0.5) {
    Eps -= 1.0;
    y ++;
}

Я немного упрощаю, чтобы не перегружать, этот алгоритм работает пока производная меньше единицы. Если производная больше единицы, нам следует использовать движение по Y. По сути мы минимизируем отклонение от уравнения.

$Eps(x,y)\; =\; A*x^2\; +\; B*x\; +\; C\; -\; y$
$Eps(x,y+1)\; :=\; Eps(x,y)\; -\; 1$
$Eps(x+1,y+1)\; :=\; Eps(x,y)\; +\; 2A*x\; +\; B$

На каждом шаге мы сравниваем две величины Eps(x,y+1) и Eps(x+1,y+1)

y ++;
Eps --;
Eps1 = Eps + 2A*x + (1 + B);
if (-Eps > Eps1) {
    Eps = Eps1;
    x ++;
}

Только что мы разобрали алгоритм для хождения по корню квадратному. Корень - сложная функция, а мы реализовали движение по обратной функции даже без деления. В общем виде алгоритмы подобного вида должны анализировать ошибку и компенсировать за счет шага в соседнюю клетку.

Дуга окружности

Аналогично мы можем вывести алгоритм хождения по дуге окружности. В качестве функции ошибки рассмотрим уравнение окружности с радиусом R. Чтобы не перегружать изложение, рассматриваем случай двжижения по часовой стрелке в первом квадранте, для производной меньше единицы.

$Eps(x,y)\; =\; x^2\; +\; y^2\; -\; R^2$
$Eps(x+1,y)\; :=\; Eps(x,y)\; +\; 2x+1$
$Eps(x+1,y-1)\; :=\; Eps(x+1,y)\; -\; 2y\; +\; 1$

x ++;
Eps += 2*x + 1;
Eps1 = Eps - 2*y + 1;
if (Eps > -Eps1) {
    Eps = Eps1;
    y --;
}

Экспонента и логарифм

Как мы ранее показали на примере параболы, нам ничего не стоит перейти от вычисления прямой функции к обратной. Но вот если прямая функция определена "криво", что делать? А что такое экспонента, как она вообще в математику попала. Её определяют через .. никак не определяют, и через разложение в ряд - криво и приближенно, бесконечно- не возможно, и через дробь - бесконечно и не возможно, через предел - бесконечно криво. Все, что связано с бесконечно малыми или бесконечно большими не применимо для вычислений. Нормально экспоненту можно определить только через дифференциальное уравнение, решением которого является искомая функция. Движение вдоль экспоненты - это решение дифференциального уравнения. Функцию ошибки введем из диф.ура.

$dy/dx\; =\; -y/T$
$Tdy\; =\; -ydx$
$Eps(x,y)\; =\; y*dx\; +\; T*dy$
$Eps(x+1,y)\; :=\; Eps(x,y)\; +\; y$
$Eps(x+1,y-1)\; :=\; Eps(x+1,y)\; -\; T$

x ++;
Eps += y;
Eps1 = Eps - T;
if (Eps > -Eps1) {
    Eps = Eps1;
    y --;
}

Тут мы сравниваем две ошибки, Eps(x+1,y) и Eps(x+1,y-1), стараемся уменьшить ошибку. Ранее мы сравнивали ошибку с 0.5, и округляли к ближайшему целому. В общем виде можно представить как минимизация ошибки (отклонения от уравнения).

Логарифм - обратная функция. Значит и вычислят ее нужно относительно оси Y

$Eps(x,y)\; =\; y*dx\; -\; T*dy$
$Eps(x,y+1)\; :=\; Eps(x,y)\; -\; T$
$Eps(x+1,y+1)\; :=\; Eps(x,y+1)\; +\; y$

y ++;
Eps -= T;
Eps1 = Eps + y;
if (-Eps > Eps1) {
    Eps = Eps1;
    x ++;
}

Синус и косинус

Возможно ли таким же способом посадить космический корабль на планету или регулировать температуру реактора? Мы можем по аналогии предложить решать системы дифференциальных уравнений. Для примера возьмем систему осциллятора.

$dy/dt\; =\; x/T$
dx/dt = -y/T
$Tdy\; =\; xdt,\; Tdx\; =\; -ydt$
$C(x,dy,dt)\; =\; x*dt\; -\; T*dy,\; шаг\; алгоритма\; dt=1$
$S(dx,y,dt)\; =\; y*dt\; +\; T*dx,\; шаг\; алгоритма\; dt=1$

На каждом шаге dt=1

$C(x,0,+1)\; :=\; C(x,0,0)\; +\; x$
$S(0,y,+1)\; :=\; S(0,y,0)\; +\; y$
$C(x,+1,0)\; :=\; C(x,0,0)\; -\; T$
$S(+1,y,0)\; :=\; S(0,y,0)\; +\; T$

Предлагаю синтезировать алгоритм самостоятельно...

Полагаю возможным синтезировать алгоритм из любой системы линейных дифференциальных уравнений.

Нахождение обратного числа

Одна из способностей, которая проявилась у меня с детства...

Пишу программы под всякую странную аппаратуру. В странной аппаратуре плохо считается операция деления. Например, берем самую совершенную, казалось бы, архитектуру Intel, в ней операция деления выполняется [AF1] очень медленно. Все арифметические инструкции, включая умножение, запускаются по 4 шт за такт, а вот деление только одно и продолжается целых 6 тактов.
Core i7 Coffee Lake: Умеет паралелить множество инструкций, а операция умножения делается только на одном из 8 конвейеров, имеет задержку 4 такта, на прохождение (Latency) и может подряд выполняться с производительностью 1 такт на умножение (Throughput). Я не беру векторные инструкции, беру простую задачу поделить одно число на другое. Деление вызывает настоящий ступор в системе, 26 тактов на загрузку инструкции (Latency) и 6 тактов зависание на конвейере.
Берем менее совершенную архитектуру, ARM Cortex, в документации указано число циклов на операцию умножения и деления, 2 и 12 соответственно. В 6 раз операция деления медленнее операции умножения. А еще есть контроллеры, которые вообще не имеют аппаратного деления. Эмуляция деления это сотни тактов процессора.

Вот, к примеру, мне понадобилось штамп времени разложить на число, месяц и год. Потом, часы, минуты и секунды. Начинаем считать: остаток от деления штампа времени на (24*60*60) - это секунды от начала дня. Потом делим на (60*60), потом на 60 ... сплошные операции деления на константу. Или берем задачу форматирования числа, надо на каждом десятичном разряде выполнить деление на 10 с остатком. Вот тут и приходит здравая мысль - это оптимизация, которая может выполняться на этапе компиляции. Целочисленное деление на константу можно заменить на умножение со сдвигом. Фактически мы заменяем деление на умножение на дробь. Не все числа "рациональные", не все обратные числа можно представить в виде дроби с достаточной точностью. Приближение первое: мы хотим представить константу в виде дроби 1/B ≈ C/2^n. Первое что пришло в голову n=32, брать только старшие 32 бита от целочисленного умножения с разрядность 32х32бит, но это так не работает. Надо умножать на самое большое число, для которого не возникает переполнение, использовать максимально возможное n, чтобы константа С годилась для всех целых чисел. Число С должно содержать 1(единицу) в старшем разряде, не меньше 0x80000000UL.
Оптимизация деления на константу на языке Си запишется так:
uint32_t Q = (A*C)>>n,
где С и n -- константы.
Для нахождения констант предлагаю алгоритм:

uint32_t div_c(uint32_t b) {// находим число С
    uint32_t C;
    int k = __builtin_ctz(b);// число ноликов сзади
    b>>=k;
    n = 63 - __builtin_clz(b);
    C = ((1ULL<<(n))/b)+1;// сдвигаем на число ноликов спереди
    n+=k;
    return C;
}

Проверить справедливость замены можно методом перебора чисел, это занимает не много времени.

uint32_t verify(uint32_t B, uint32_t C, int n) {
    uint32_t A;
    for (A=(~0UL); A!=0; --A){// все числа 32 бит
        uint32_t Q = ((uint64_t)A*C)>>32>>(n-32);
        if (Q != (A/B)) {
            break;
        }
    }
    return A;
}

Примеры таких констант Q=A/B = (A*C)>>n:
 

Q = (A* 0xCCCСCСCDULL)>>35; // Q=A/10 кратно /5 работает для всех A
Q = (A* 0xCCCСCСCDULL)>>34; // Q=A/5 работает для всех A
Q = (A* 0xAAAAAAABULL)>>33; // Q=A/3 работает для всех A

B=  3: 0xAAAAAAAB n=33
B=  5: 0xCCCСCСCD n=34
B=  7: 0x92492493 n=34 Q=A/7 для 31 бит.
B= 60: 0x88888889 n=37
B= 10: 0xCCCСCСCD n=35
B=100: 0xA3D70A3E n=38
B=1000: 0x83126E98 n=41
B=3600: 0x91A2B3C5 n=43
B=86400: 0xC22E4507 n=48
B=1000000: 0x8637BD06 n=51
B=365: 0xB38CF9B1 n=40 Q=A/365 для 31 бит.
B=153: 0xD62B80D7 n=39
B=255: 0x80808081 n=39

Некоторые константы нельзя представить в виде 32 битного умножения, точности не хватает. Для 31 битных целых чисел всегда хватает точности.

-- Магия чисел!

[AF1] https://agner.org/optimize/instruction_tables.pdf

Электронное правительство: настройка сервисов

 Мы по роду деятельности занялись "чисткой" в правительстве. Пишем запросы и анализируем ответы из правительства, потом пишем еще запросы и анализируем систему в целом. Систему в целом называем "электронное правительство" - подходящий термин.

Что это такое. Это будущее нашего общества. В этой системе человек - управленец, член правительства, чиновник всего лишь исполнитель в живой системе регламентирующей работу правительства. Система предоставляет интерфейс каждому участнику информационного обмена, накладывает свои ограничения. Можно сказать это сеть с элементами ИИ. Интелект в ней выражен слабо, но даже сама система взаимодействия и учета обращений влияет на решения, на способ принятия решений.

Структура сети

Работа чиновника выглядит так. На работу ходить не обязательно. Есть возможность сидеть дома и переписываться через интернет, работать удаленно.

mail.kodeks.vpn (Postfix) with ESMTP -- Постфикс мы уважаем, но по сути это сервер VPN на базе Linux, сервер осуществляет удаленный доступ. mail.kodeks.vpn (unknown [10.30.3.73]) Слово Кодекс в контексте не нравится. Проблема в том что ВСЕ правительство, все комитеты (в SPB) работает через один IP адрес [10.128.66.165] через один сервер [10.30.3.73]. Выход из строя или неправильная работа этого адреса - проблема для всей сети. Пользователи сети никак не отличаются, нельзя выделить источник по IP адресу. Аутентификация пользователей в Postfix по паролю или сертификату безопасности при отсылке сообщений по SMTP не производится. Сервер на нижнем уровне позволяет скрыть источник данных и не проверяет аутентичность сообщений. unknown [10.128.66.165], обратные адреса во внутренней сети не различаются. Соответственно, правила фильтрации трафика в Postfix не настроены.

В системе развернуты два сервиса проверки сообщений на вирусы

X-Antivirus: Dr.Web (R) for Unix mail servers drweb plugin ver.6.0.2.8
X-Antivirus-Code: 0x100000

X-KLMS-Rule-ID: 3
X-KLMS-Message-Action: skipped
X-KLMS-AntiSpam-Status: not scanned, whitelist
X-KLMS-AntiPhishing: not scanned, whitelist
X-KLMS-AntiVirus: Kaspersky Security 8.0 for Linux Mail Server, 
    version 8.0.1.721, not scanned, whitelist

Для проверки трафика на вирусность используется сервер
mail.smolny.uts (mail.cn.uts [10.20.20.3]) Все работает на Postfix один из сервисов работает, как Milter с пересылкой на localhost.
Сервер ничего не проверяет, вообще ничего, все письма проходят по белому списку, список настроен по IP адресу, а IP адрес у всех один и тот же.

mail.gov.spb.ru (mail.gov.spb.ru. [176.97.35.9]) -- это внешний интерфейс системы, через него осуществляется выход наружу из приватных сетей Правительства (СПб) в сеть интернет.

Результат проверки на вшивость исходящих сообщений:
Received-SPF: softfail (google.com: domain of transitioning noreply@letters.gov.spb.ru does not designate 176.97.35.9 as permitted sender) client-ip=176.97.35.9;
Authentication-Results: mx.google.com;
       spf=softfail (google.com: domain of transitioning noreply@letters.gov.spb.ru does not designate 176.97.35.9 as permitted sender) smtp.mailfrom=noreply@letters.gov.spb.ru

Проще говоря все иходящие сообщения классифицирются как убогая попытка навредить простому пользователю, потому что не проходят проверку. Гугл классифицирует их как "опасные", не проверенные, разве что в спам не перекладывает.

Фильтрация на основе SPF записей -- это старый и весьма простой механизм проверки от подмены источника сообщений.

В современных системах корпоративной почты используется механизм аутентификации серверов DKIM + SPF, используется цифровая подпись DNS зоны DNSSEC. Все это поддерживается в связке BIND 9 + Postfix + OpenDKIM.

Если оценивать работу по созданию сети - двойка, она плохо сделана. Я напишу следующим сообщением, как сделать правильно. Но пока что вид этой системы ужасен. Она не защищена, она подвержена вирусным атакам, атакам хакеров, полна уязвимостей и ошибок настройки.

Регламент

Что должен делать чиновник. Чиновник хочет набивать себе рейтинг. Когда чиновник это понимает, он становится уязвимым. Обычно чиновники, которые понимают, что продвижение по службе напрямую связано с социальными сетями, создают себе среду общения помимо сайта правительственного комитета, в соц сетях. Большой популярностью пользуются интаграмы и телеграммы. Потом все спускается до уровня желтой прессы (онлайн публикации) и сети ВКонтакте.
Как только правительственный комитет или отдельный чиновник создает свою среду общения -- это поле действия троллей. Стадо тролей формирует решения правительства.

По теме регламента хочу высказатся, но формат сообщения тесен. Выскажусь отдельно. Обозначил уязвимость. Взломать сеть с человеком в узле сети и обратной связью через соц сети проще всего через этого человека. Технологию взлома описать могу, но задачу вижу в обратном, как защитить от этого.

Чего почитать простому админу перед увольнением:

https://ru.wikipedia.org/wiki/Sender_Policy_Framework

https://ru.wikipedia.org/wiki/DomainKeys_Identified_Mail

https://ru.wikipedia.org/wiki/DNSSEC

Дезинфекторы

У нас на производстве стали плодиться дезинфекторы. Думаю, если пойдет так дальше, под дезинфекторы можно выделить отдельный раздел.

Мобильный дезинфектор

Это такое устройство с двумя колесиками, которое распыляет адскую смесь (дезинфектор) в воздухе. Для распыления используется компрессор на десять атмосфер. Воздух под давлением подается в форсунку, где смешивается с жидкостью и выходит наружу в виде струи (факела). Близким по принципу работы устройством является - краскопульт для нанесения краски.
Отдадим должное краскопультам. От краскопультов взяли конструкцию форсунки. Форсунки бывают разных видов: HP, HVLP... HP (High Pressure) – высокое давление. HVLP (High Volume Low Pressure) - высокий объем, низкое давление. Мы работали с обоими типами. В серию пошли форсунки высокого давления, потому что нужно было обеспечить дальнобойность. Факел получили длиной 3-4метра. Однако, форсунки низкого давления тоже имеют право на существование, когда необходимо обрабатывать поверхности с расстояния до 1 метра.
По заданию, устройство должно работать в двух или трех режимах, по расходу дезинфектора (хим. раствора): "туман", "увлажнение", "орошение",.. "автомойка". Регулирование расхода химии выполняется с использованием маленького дозирующего насоса: мембранного или перистальтического. Подача воздуха от компрессора - через клапан электромагнитный. Устройство во время работы подсвечивает факел узконаправленным светом, мощным светодиодным светильником встроенным в форсунку - это для удобства, чтобы факел был виден.
Устройство включает сенсорный графический интерфейс (TFT-дисплей с тач-панелью) на контроллере. Рассчитывает время и циклы обработки по объему помещения и норме расхода. Пишет файл журнала.
Устройство может применяться для обработки общественных помещений, контейнеров, грузов, транспортных средств.

Стационарный дезинфектор для мобильного пункта КТ

Представляем себе медицинскую установку, где нужно просвечивать (диагностировать) заразных больных. Установка монтируется в трех помещениях - два тамбура (вход, выход) и собственно установка. После каждого заразного посетителя, выполняется дезинфекция последовательно каждого из трех помещений. В каждом помещении монтируется настенный блок форсунок с подсветкой факела. После хим. обработки включается вытяжная вентиляция и зажигаются информационные таблички "не входить", "дезинфекция". Последовательности обработки (циклы) запускаются с пульта оператора. Установка работает по тому же принципу, что и мобильный дезинфектор, только на три группы форсунок и на два компрессора, а также выдает сигналы управления на вент. систему и систему контроля доступа. Ведет журнал.

Проходной шлюз для хим. обработки сотрудников

Это другая технология. В основе лежит концепция адиабатических систем увлажнения воздуха с распылением жидкости под высоким давлением в 30 атм. В системе используются специальные мини форсунки расположенные рядами сверху, снизу и по бокам шлюза, создают облако тумана вокруг объекта. Шлюз работает в автоматическом режиме по датчику присутствия и двери. При закрытых дверях включается обработка на заданный интервал. Шлюз имеет систему дренажа, отработанная жидкость (конденсат) собирается в бак. Объем шлюза подсвечивается.
Шлюз - мобильный, собирается как туристическая палатка с тентом на каркасе.
Используется по назначению для обработки персонала в защитных костюмах.

UV-C дезинфектор отработанного воздуха

Это перспективная разработка, выполняется по заказу медиков. Основана на новой технологии светодиодов диапазона UV-C (жесткий ультрафиолет). Пока что у светодиодов UV-C (255нм, 275нм) низкая квантовая эффективность и низкий показатель срока службы в сравнении со светодиодами видимого диапазона. Однако, технология не стоит на месте, мы ожидаем, что уже через год светодиодные систему УФ дезинфекции воздуха будут превосходить аналогичные люминесцентных лампах, как это было со светодиодным освещением. UV-C излучение убивает вирусы с высокой эффективностью. Система которую мы проектируем обрабатывает вдыхаемый/выдыхаемый воздух с эффективностью от 90% до 99%. Заказана система (приставка) для обработки отработанного воздуха в установку ИВЛ. Система монтируется в "выхлопную" трубу (трубку), представляет собой линейку светодиодов с последовательным запуском. Светодиоды включаются в момент выдоха и подсвечивают "бегущей волной" убийственного света выхлоп воздуха внутри трубки.
Задача - убить всех микробов и вирусов на выдохе, с одного прохода воздуха. Никакая система УФ дезинфекции на люминесцентных лампах не может обеспечить компактности. Данная технология позволяет делать носимое оборудование и встраивать UV-C дезинфекторы прямо в респиратор. Сегодняшний уровень технологии UV-C LED (УФ светодиодов) позволяет это сделать. Стоит дороже ватно-марлевой повязки. НО предполагаю, что к концу года цены станут адекватными, чтобы за 30-50у.е можно было выпустить маски со встроенным УФ-дезинфектором.
На сегодня мы запустили в производство опытные экземпляры электроники: регуляторы на 3 зоны облучения и 9 светодиодных линеек с диммированием со стабилизацией тока светодиода, светодиодные модули на UV-C - платы на металлическом основании. Кроме того, подготовили к выпуску модуль светодиодный для UV-C линз LEDIL. Линзы позволяют сфокусировать излучение и использовать УФ-дезинфектор для обработки продуктов на конвейере. Получается УФ-бактерицидная завеса.

Есть потребность? Обращайтесь. Я чувствую, в нашем арсенале не хватает еще одного типа дезинфектора.

Почему оптимизация memset накрылась...

Некоторые вещи совсем не такие как кажутся. Я написал реализацию memset с разными наворотами по оптимизации, а она не работает. Исследовал ассемблерный код, оказалось, компилятор на свое усмотрение вставил внутрь моей функции обращение на функцию memset, потому что нашел похожий цикл и решил его оптимизировать таким образом.

Такую же причуду удалось получить на функции memcpy. GCC чудит и внутрь вставляет рекурсию, функция вызывает себя. Это происходит при использовании оптимизации -O3.

Отключить оптимизацию можно ключом -fno-tree-loop-distribute-patterns.

ELF32 для ARM Cortex-M

Мы изучили идеи, которые вложены в загрузчик GNU/Linux. Поигрались с возможностями компилятора (gcc, clang) и линковщика (ld). Готовы описать, как выглядит сборка проекта и как ее упростить. Наша цель встроить в контроллер ARM Cortex-M4 функцию динамической загрузки приложений и загрузку динамических библиотек. Зачем? Чтобы менять программу в процессе работы. Я вынашиваю идеи как делегировать на контроллер обработку данных.

[IHI0044] ELF for the Arm Architecture
ELF format
ELF32 -- бинарный формат для представления объектных и перемещаемых файлов, исполняемых файлов, разделяемых данных и динамических библиотек. Формат состоит из разделов (сегментов). Исполняемый файл может содержать загружаемые сегменты (программы). Сегменты содержат: таблицы символов, строки с именами объектов и функций, а также необходимые данные для сборки кода (таблицы перемещений).
Таблица перемещения - описывает, как нужно модифицировать переменную или вызов функции, с учетом того, что на этапе компиляции не определены абсолютные адреса переменных и адреса функций. Т.е адреса должны подставляться в скомпилированный код на этапе сборки. Фактически код после компилятора представляет из себя шаблон, в который нужно вписать ссылки. Для каждой целевой платформы определяется, как именно вписывается ссылка в сегмент кода и сегмент данных - правила модификации кода. Наша целевая платформа - ARM с системой команд Thumb32. Арм определил ряд правил сборки кода [IHI0044]. Этот список содержит около сотни разных правил. Правила могут быть сложные, сложнее, чем просто записать адрес по указанному смещению. Обычно правила выглядят примерно так: Взять содержимое инструкции, декодировать инструкцию, к аргументу инструкции добавить смещение - адрес сегмента, вычесть адрес самой инструкции, и закодировать инструкцию обратно. Переменные (данные, data) и функции (код, text) могут размещаться в разных сегментах, поэтому при сборке возникают дополнительные операции.
Мы действуем методом обратной разработки. На входе уже есть готовый ELF формат с таблицей перемещений. В формате используются всего четыре разные правила. Заметим, что загрузчик исполняется в составе операционной системы под совершенно определенную архитектуру. Мы будем обрабатывать только те правила, которые возникают на данной архитектуре. Таким образом, число правил существенно уменьшается. Получаем всего 2 правила сборки:
R_ARM_ABS32 -- это правило абсолютного перемещения. Data: (S + A) | T. Сложить содержимое ячейки и адрес сегмента. Для адреса функции не забыть правильно указать флаг системы команд.

R_ARM_THM_CALL -- это правило кодирования инструкции вызова функции Thumb32: ((S + A) | T) - P (маска=0x01FFFFFE) \sa R_ARM_THM_PC22. Сложить содержимое ячейки и адрес сегмента и вычесть адрес самой ячейки. Для ссылки на функцию добавить флаг системы команд Thumb - единичку в младшем разряде. Такое же правило форматирования используется для вызовов R_ARM_THM_JUMP24. Тут мы используем некоторое упрощение- длина вызова - 22 бита вместо 24, два бита не обрабатываем. На вопрос почему, ответ: потом что так обрабатывает линковщик GNU binutils, такое упрощение рекомендует ARM.

Компилятор GCC использует правило R_ARM_TARGET1 для формирования таблицы инициализации - таблицы конструкторов и деструкторов. Это правило может быть таким же, как и R_ARM_ABS32, мы определяем как выглядит это правило, потому что инициализация - это дело разработчика операционной системы, наше дело. Мы используем тот же метод, R_ARM_ABS32.

Компилятор Clang использует еще пару правил. Эти правила возникают из идеи грузить константы 32 бита в два приема - отдельно младшую (lower16), отдельно старшую часть (upper16).

Сделал утилиту, которая работает в точности как readelf (GNU binutils), разбирает таблицы символов и перемещений. Зачем сделал, не очень понимаю. Результатом является возможность реализации динамической загрузки и динамической линковки кода в контроллере, разбор elf формата. Практического приложения пока нет. Пока разбирался с возможностями линковки увидел возможность собирать операционку с использованием статических библиотек. Статические библиотеки можно прикомпиливать целиком или только те фрагменты, которые используются в сборке, на которые ссылается код. Таким образом без ущерба для целостности удалось ужать объем ядра. Если функции не используются они в образ не попадают.

DSP на OpenCL -- строительные блоки и блочные диаграммы

Но по сути, мы тут не про язык разговариваем. У меня копится материал для изложения, который я выкладываю для обсуждения. Первая часть изложения - про объекты в протоколе и в описании модели. А вторая часть продолжение темы выкручивания алгоритмов DSP для примения в составе блочной диаграммы.

Блоки в языке OpenCL C - это такие чудные вложенные функции со шляпкой. В GCC поддерживается расширение языка Си, т.н. "nested functions", похожие сущности -- гнездящиеся функции. В языке OpenCL C 2.0+ можно на стороне устройства описывать из блоков асинхронный процесс обработки.

Достаточно крупные операции в DSP надо делать inline функциями, вернее давать возможность компилятору оптимизировать(векторизовать) большие блоки кода. Один из основных методов дающих существенный прирост производительности - векторизация циклов. Это значит что одиночные циклы, для которых число итераций определяется снаружи следует писать в виде inline функций. Мне нравится набор функций, который предлагает ARM CMSIS DSP. Но есть оговорки и вопросы оптимизации под аппаратуру. У нас есть задача переносить коэффициенты и модели из настольного компьютера в контроллер. В компьютере мы используем векторизацию float, в устройстве управления и сбора данных, сервере автоматизации используем ARM Neon, планируем использовать OpenCL. Нам нужен объект и формат данных для переноса "тензоров" и организации "потока тензоров" средствами протокола обмена, между платформами, нам нужен единый API (оптимизированный под конкретную архитектуру) для представления блочных диаграмм. Концептуально, мы говорим про внешний интерфейс для представления функционального блока FunctionalBlockObject, объекты-контейнеры данных TensorObject. А также мы будем рассматривать некоторый набор имен программных блоков, представленных в библиотеке DSP, чтобы ссылаться на их использование в блочной диаграмме.
Говоря про формат данных для внешнего представления блочных диаграмм, мы на сегодня будем ориентироваться на форматы принятые в BACnet: правила кодирования ASN.1, формат Json и CSML. Эти форматы мы выбираем прежде всего, чтобы не плодить сущности, поддержка этих форматов уже присутствует в составе нашего ПО.

Тензоры

Тензор - это массив данных определенного типа: float, double, int, char. Мы говорим про внешнее представление данных. Тнезор обладает свойством выравнивания данных - это его внутреннее свойство, определяется автоматически при создании объекта. Тензор имеет порядок укладки данных при записи и чтении, формат записи. Порядок записи включает: число каналов (feature), пакет данных (batch), пространственную размерность (spatial). Например, изображение с камеры имеет размерность 2d (spatial), организовано как поток кадров (batch), может иметь несколько каналов (feature). Звук имеет размерность =1 (spatial), организовано в поток по времени (batch), и разделено на каналы (features). Тензор - это единица обрабатываемой информации, с точки зрения функционального блока DSP или NN.
Мы будем исходить из того, что передать тензор целиком в одном пакете может оказаться не возможно. Поэтому обращение к тензору может быть как к массиву, ReadRange - запрос на чтение фрагмента массива. Мы предполагаем некоторую процедуру заполнения входных данных, объектов связанных между собой блочной диаграммой, затем запуск преобразования. Результатом преобразования может являться набор тензоров. Результат преобразования может распространяться по подписке CoV. Преобразование запускается по готовности входных данных, т.е. когда все входные данные(тензоры) записаны.
Тензоры могут быть вида TensorOutputObject, TensorInputObject. TensorOutputObject - обладает командным свойством на PresentValue. Когда записывается содержимое тензора, происходит запуск зависимостей по готовности.

Функциональные блоки

Функциональный блок содержит ссылку на исполняемый код(kernel) - DeviceObjectReference, список аргументов, список фиксированный идентификаторов объектов ARRAY_OF(DeviceObjectReference) - зависимости. В процессе исполнения, блок оформляет подписку на соответствующие объекты списка зависимостей. Функциональный блок имеет статус(состояние,контекст) - это некоторая структура данных, в которой могут хранится промежуточные величины. Контекст сохраняется и может быть перезаписан в режиме out-of-service.
Для блока мы определяем фазы: Инициализация, обновление контекста, обработка, пауза/завершение/сериализация контекста. Блочная диаграмма это не сам конвейер, это пакетное задание, которое может выполняться на конвейере с использованием данных. Конвейер это очередь исполнения по готовности.
Функциональный блок может обладать отладочной информацией (опция), для отладки используются штампы времени: queued, submit, start, end.

Программы

Программа - это текст или бинарник. Со стороны хост-приложения возможно определить из бинарника список блоков и список агрументов(входных/выходных портов). Каждый порт описывается 'форматом записи', однако формат записи из программы не определить.

Строительные блоки

Список функций API

dot(a,b)

операция свертки вектора sum_{0}^{N-1}(a[i]·b[i])

conv(a,b,n)

операция частичной свертки, выполняется с разворотом вектора sum_{0}^{N-1}(a[i]·b[n-i-1]). В это определение попадает корреляционная функция

float cascade_biquad_df2T(z,x)

вычисление значения каскада y = z+b0·x

float cascade_biquad_df2T_update(S,x)

обновление регистров каскада (S)

float fir(S,x)

FIR фильтр. Интерполяция.

pid(S,x)

PID регулятор.

lms_update(S,x)

LMS подстройка параметров адаптивного фильтра

IIR фильтры обрабатывают batch составляющую, время.
Для задач мультирейт используются фильтры LPF_decimate (по времени).
Аудио процессор может обрабатывать полосы и сшивать их на выходе. Для этого используются фильтры Allpass. В каких-то случаях могут использоваться фильтры iir_lattice.
Пид регулятор - это фильтр типа biquad. LMS фильтр - подстройка.

PID регулятор

 

Передаточная функция:
H(s) = ( K_P + K_I·1/s + K_D·s ) Замена: 1/s = T/2·(1+z^-1)/(1-z^-1), s = 1/T·(1-z^-1)

Передаточная функция в дискретном пространстве:
H(z) = KP + KI·T/2·(1+z-1)/(1-z-1) + KD/T·(1-z-1)
или 
H(z) = KP + KI·T·1/(1-z-1) + KD/T·(1-z-1)
Ki := KI·T
Kd := KD/T
Может быть представлена биквадратной секцией

void pid_init(S, x){
  S->b0 =  Kp + Ki + Kd;

  S->b1 = -Kp -2Kd
  S->b2 =  Kd;

  S->z1 = 0;
  S->z2 = 0;
}
// первый проход
float pid(S, x){
  return b0*x+z1;
}
// второй проход, обновление регистров
void pid_update(S, x){
  z1 =(b1-b0)*x + (z2 - z1);
  z2 = b2*x;
}

При разработке PID регулятора мы также используем два прохода: первый проход встроен в поток обработки, второй - поток обновления регистров и состояния фильтров. Пока что у нас получается что абсолютно все фильтры представлены выражением: y = g*x+Z, включая и PID регулятор. Далее мы хотим добавить свойство автоматической подстройки каэффициентов FIR фильтров и IIR фильтров. На втром цикле обновления регистров, мы добавляем возможность подстройки коэффциентов по методу LMS (). Есть известное преобразование FIR фильтра в LMS - получается адаптивный фильтр. Мы создаем сеть, в которой каждый функциональный блок должен обладать адаптивностью. Точнее можно сказать, что в процессе работы возникают периоды обучения - подстройки коэффициентов модели. Таким образом, фаза UPDATE может сопровождаться "обучением", если известна величина ошибки выходного сигнала. Для каждого слоя сети, мы можем определить этот признак "обучения".

LMS фильтры

Фильтры адаптивные (LMS) мы будем изготавливать из фильтров типа IIR и FIR. Метод LMS можно применять для обучения (подстройки весовых коэффициентов) нейронной сети. Мы вводим единую методику обучения/распознавания для нейронных сетей (NN) и для структур цифровой обработки сигналов (DSP). Нам известен способ изготовления адаптивного цифрового фильтра из FIR фильтра эту методику мы хотим расширить на остальные задачи.

Для некоторого преобразования c передаточной функцией представленной полиномом H(z) = h₀+h₁z^-1+h₂z^-2+...+h_Nz^-N , можно подстраивать коэффициенты, если известна ошибка выходного значения. Ошибка может быть пересчитана в поправку каждого конкретного коэффициента.
Ошибку на выходе определим, как квадрат отклонения.
E = (d[n] - y[n])² = (d[n] - sum(b[i]z^-i))²
изменение коэффицента для фильтра можно определить как градиент. Используем метод "градиентного спуска"
w[n+1]=w[n]-μ·∂E/∂w
Здесь μ - это величина шага подстройки. Для стабильного проявления методики, бывает полезно ограничить ошибку в каких то пределах, используя функцию clamp(). Берем частную производную, не сильно увлекаясь частностями. w_i[n+1] = w_i[n] - 2μ·e[n]·∂e[n]/∂w_i
∂E/∂w_i = -2(e[n])(x[n-i])

b_i[n+1]=b_i[n]+2μ (e[n])(x[n-i]).
Это все! Каждый коэффицент подстраиваем исходя из ошибки на выходе. IIR фильтр - это комбинация двух фильтров FIR. Для подстройки коэффициентов A(z) в IIR-фильтре с передаточной функцией H(z)=B(z)/A(z) используем аналогичный вывод:
a_i[n+1]=a_i[n]+2μ (e[n])(y[n-i]).

{Тут в изложении присутсвует некоторое искусство, с которым надо поразбираться. Работать будет в любом случае, однако математически правильный вариант брать частную производную не от уравнения в конечных разностях. Варианты, которые можно получить исследуя конечные разности и интегралы от дельта-функций - это линии задержки разного вида и фильтры на поток ошибок. К сожалению, быстро ответ не нашел. Нашел, что этим когда-то занимался I.-D. Landau, }
{1976 Feintuch’s algorithm}
{A parallel-type adaptive algorithm is proposed which utilizes the fast least-squares method. Its computational complexity is much less than that of I. Landau's (1978) method, which is based on hyperstability theory Hyperstability requires much computation because it involves matrix operations. The proposed method has nothing to do with hyperstability. It is also shown theoretically and using computer simulation, that the convergence performance of the proposed method is better than that of the series-parallel-type fast least-squares method.} Линия задержки будет разная для разных форм представления фильтров. Глядя на презентацию, мне почему-то кажется, что тут может быть ошибка в интерпретации, что-то не то с частной производной. Должна быть простая форма. Мне видится простая форма при вторичном использовании регистров z. Предположительно выглядит так, доказать надо на практике:

void lms_dt2t_update(S, x, ue){
  b0+= ue*x;
  b += ue*x;// вектор
  a += ue*y;// вектор
}
void lms_update(S, x, ue){
  b0+= ue*x;
  b += ue*z;// вектор
  a += ue*z;// вектор
}

Если мы применяем LMS к фильтру типа PID должны быть веса разные для коэффициентов. Коэффциенты A не подстравиваются.

DSP на OpenCL - Изоморфные преобразования алгоритмов

Хочу поделиться знаниями, вернее акцентировать внимание на известном факте.. Каково место цифровой обработки сигналов в коде. Хотим затолкать цифровую обработку в поток OpenCL, выполнять обработку на потоке данных. При этом не дает покоя одна мысль. Мы хотим получить наивысшую скорость работы и малые задержки. Поэтому мы каждый алгоритм DSP хотим разделить на две части. В первой части рассчитываем результат за минимальное число операций, во второй обновляем значения переменных. Я начну писать, потом видно будет.
В разделе DSP есть два вида фильтров: IIR- и FIR- фильтры. Прежде всего, оговорюсь все это относится к анализу LTI-систем, для которых можно описать передаточную функцию Y(s)=H(s)X(s) в непрерывном виде и далее перейти к дискретному виду передаточной функции H(z) путем замены переменной s←2/T(z-1)/(z+1). Передаточную функцию можно представить в виде отношения полиномов B(z)/A(z). Т.е.в виде дроби (дробно-рациональной функции) - сверху и снизу дроби полином z. Причем буква Z^-1 на самом деле представляет из себя оператор задержки в дискретном по времени процессе. Как вообще люди в процессе своего образования доходят до этого - загадка. Думаю все сознательные электронщики и программисты должны это знать, но полагаю мало, кто знает. Наше образование не было полным в том виде, в каком оно может служить инструментом программиста или электронщика. Статья для избранных. На самом деле я уже начинаю сомневаться, что вообще этому учат. Когда-то учили анализу систем, учили передаточным функциям. Предлагаю, сейчас найти учебник на английском (по теме Linear time-invariant system и Digital Signal Processing). Для работы, чтобы получить готовый набор коэффициентов использую GNU Octave или MATLAB с модулем Signal, он умеет готовить матрицы коэффициентов. Использую конспекты лекций по курсу DSP & Digital Filters, потому что мне это близко и понятно, именно в таком виде. Автор курса ссылается на учебник.
[#] "Digital Signal Processing" Sanjit K. Mitra, 4th edition, McGraw Hill, 2011. ISBN 0071289461
Для стационарных систем (LTI) передаточная функция — это дробно-рациональная функция комплексной переменной s. Тернистый путь познания лежит через преобразования Фурье и Лапласа. Однако более короткий путь можно найти через дифференциальные уравнения в конечных разностях, только этот путь неведом выпускникам со специальностью кибернетика, так учат физиков. У меня в образовании был курс ТФКП(теория функции комплексного переменного) и курс математической физики (который символизирует наезд дельта функцией на уравнения), от которого ничего тут использовать не буду.
1) Систему можно представить в виде дробно рациональной функции N-ого порядка в странном пространстве наполненном операторами задержки и умножителями, -- это понятно программисту. Причем порядок числителя не выше чем у знаменателя. 2) Безумную дробь можно разложить на полюса и нули(полюса - это решения полинома в знаменателе, нули - решение полинома в числителе), путем факторизации полинома(еще одно умное слово - разложить на скобки, - так говорят в школе). Длинную дробно рациональную функцию большого порядка можно представить в виде суммы или произведения этих самых дробно-рациональных функций второго порядка. (точка!! - никакой больше теории, только картинки).
Иногда я чувствую, что являюсь хранителем некоего сокровенного невербального знания :). Могу доказать теорему не произнося слова, а рисуя только квадратики, треугольнички и стрелочки. Передаточные функции в дискретном пространстве можно строить в виде графов и представлять математические преобразования над функциям, как тождественные преобразования графов. Граф в точности отражает архитектуру программной или аппаратной реализации алгоритма цифровой обработки. На картинке буквой Z обозначаем оператор задержки, фактически это будет переменная (буфер, в аппаратуре - D-триггер), в которой хранится значение с предыдущего шага обработки.

Рис.1 Биквадратный фильтр. Прямое представление 1-типа DF1 (слева) и прямое представление 2-типа DF2 (справа)

Рисунок #1 получен путем прямой записи выражения B(z)X = (b₀+b₁·z^-1+b₂·z^-2)X и затем выражения A(z)Y = (1-a₁·z^-1-a₂·z^-2)Y, где z^-1 - оператор задержки на такт.
В первом случае (DF1)сложность, 5 умножений и 4 сложения: 5m+4a. Во втором (DF2) сложность та же, но для получения хранения промежуточных значений достаточно всего двух регитров Z.

Рис.2 Биквадратный фильтр. Прямое представление 2-типа DF2 (слева) и прямое представление второго типа транспонированное DF2T (справа)

Метод Транспонирования цифрового фильтра:
1) Меняем направление обхода, все стрелочки и треугольники разворачиваем. 
2) Слева будет выход, справа вход. Меняем местами буквы X и Y.
3) Разворачиваем буферы Z.
4) Где были узлы ставим "плюсик", где плюсики - ставим узел.

Цель можно считать достигнутой, мы развернули фильтр таким образом (DF2T), что на первом проходе можно получить в одно действие результат: Y = b₀·X+z₀ От входа X до выхода Y одно суммирование и одно умножение. Сложность первого прохода: 1m+1a. Этот проход совершается в той же самой математике, что и процесс свертки слоя нейронной сети.
К чему все это?. А, к нейролизации цифровой обработки сигналов в дискурсе для непосвещенных. Все что ниже первой линии будем считать частью процесса обучения, т.е. расчитывать и обновлять значения Z будем на втором проходе сети.
Какие у нас открываются возможности при использовании параллельной архитектуры. Правильно, фильтры могли бы считать паралельно, а не последовательно. Привычное разложение передаточной функции высокого порядка - в каскад (произведение) фильтров второго порядка. Каскад - это последовательная обработка фильтров, предполагает загрузку одного ядра/потока. Возможно представление в виде суммы, можно разложить в сумму фильтров первого и второго порядка. Cмотрю на структуру каскада фильтров. Каскад расчитывается, как sum(z_1k+b_0kX). Переобозначим переменную, S=sum(z_1k) -- сумму можно расчитывать на втором проходе.

Рис.3 Каскад биквадратных фильтров.

Получаем финально такой результат: каскад фильтров можно представить на первом проходе Y =Z+ gX. Весь фильтр в одно действие!

// Алгоритм 
float cascaded_iir_df2t(float x){
// первый проход
   y = g*x+s;
   return y;
}
float cascaded_iir_df2t_update(float x){
// второй проход, вычисляем s
   s=0;
   x=g*x;
   for (i=0; i<len; i++){
     y = x+z1[i];
     z1[i] = b1[i]*x - a1[i]*y + z2[i];
     z2[i] = b2[i]*x - a2[i]*y;
     s+=z1[i];
     x = y;
   }
   return s;
}

Преобразования фильтров

Рис.4 Тождественные преобразования. a) замена переменных, b) объединение идентичных буферов, c) свойство линейности преобразования.

Предлагаю для практики проделать преобразования фильтров. На рисунке #5 привожу последовательное, шаг за шагом, преобразование фильтра Allpass первого порядка из одной формы в другую. Считается, что каждый студент прослушавший курс лекций должен понимать, как проделать подобный переход.

Рис.5 Преобразования фильтра Allpass

На рисунке #6 представлена одиночная операция транспонирования над одним каскадом фильтра FIR.

Рис.6 Преобразования фильтра FIR. Транспонирование каскада.

Векторизация фильтров

Следующий пункт - оптимизация под оборудование. Возможно будет лучше считать в векторном типе с использованием явной векторизации. Исходно мы используем транспонированную форму фильтра.

Рис.7 Прямая и транспонированная форма FIR-фильтра

Ниже пример реализации FIR фильтра. Также разделен на два прохода.

// FIR фильтр с явной векторизацией
float  fir_dft(float x){
  y = g*x+z.s0;
  return y;
}
float4 fir_dft_update(float4 z, float x){
  Z0=(0.0f);
  z = shuffle2(z,Z0, (int4){1,2,3,4});
  z =z + H*x;
  return z;
}

В данном варианте расчета, для обновления регистров фильтра нужно всего две процессорных инструкции shuffle и fma.

Функция активации в слое нейронной сети

В статье дано описание функций активации. Выбран класс гладких функций удобный для реализации на CPU с поддержкой инструкций AVX512 и на GPU Intel Gen8-Gen11. При работе с GPU мы ориентируемся на язык OpenCL C. Дается некоторое количество утверждений, основанных на предположениях автора. Мы бездоказательно утверждаем, что использование класса гладких Smoothie-функций дает достаточную точность, для получения адекватных результатов работы сети.

Применяют два варианта функции активации в промежуточных слоях, остальные сводятся к производным. Мы хотим обобщить понятие о функции активации. В обобщенном виде к функции предъявляется ряд требований, таких как гладкость, монотонность и уровни насыщения. Функция задана на области определения и насыщается при определенных значениях. Важен внешний вид функции и важно, чтобы производная функции работала, давала соответствующий градиент в правильном направлении. Величина градиента не сильно важна и сказывается только на времени сходимости при обратном распространении ошибки.
Вариант 1) Сигмоида. Функция типа ступенька с размытыми краями. В обобщенном виде сигмоида может быть заменена на полное отсутствие сигмоиды лишь бы насыщалась на уровне 0 и 1. Т.е. вполне реально активацию можно заменить на операцию умножения с насыщением. Производная сигмоиды: s'(x) = s(x)(1-s(x)) выражается через значение самой функции, т.е. не надо знать ничего, кроме значения на выходе.
Вариант 2) Тангенс гиперболический. Это такая функция, которая монотонно возрастает имеет один перегиб. Имеет область значений [-1,+1].Все что реально нужно знать про эту функцию - она монотонная, нечетная и производная этой функции: (1+t(x))(1-t(x)). Тангенс гиперболический можно выразить через сигмоиду и наоборот. По сути это одна и та же функция.
Надо ли говорить, почему функция сигмоида и тангенс гиперболический не подходит под описание?! Потому что мы говорим про насыщение, а насыщение у сигмоиды не наблюдается. Это значит что нейрон будет "обучаться"(подстраивать коэффициенты) только в области, где производная не равна нулю.
Давайте предположим, что традиция использовать экспоненту в функции обусловлена исключительно требованием гладкости и дифференцируемости функции, которая в свою очередь продиктована методом вычисления градиента. Давайте предположим, что нам удаться сбалансировать систему таким образом, чтобы она не уходила в насыщение в процессе обучения.

tanh(x) = (1-e-2x)/(1+e-2x)
sigm(x) = 1/(1+e-x)
relu(x) = ln(1+ex) -- SmoothReLU, softplus, выпрямитель с гладким переходом.

Следует отметить, что производная от SmoothReLU дает сигмоиду. Функцию tanh можно выразить через сигмоиду и наоборот:

tanh(x) = (1-e-2x)/(1+e-2x) = 2sigm(2x) - 1
sigm(x) = 0.5*(tanh(x/2)+1)

Может правильнее было бы сказать, решением какого дифференциального уравнения являются эти функции. Тут самое время включить мозги, алгоритмы обучения сводятся к минимизации ошибки. Функции активации можно вводить не аналитически, а через уравнение. Если для каждого шага обучения можно оценить величину ошибки, функция ошибки может вводится, как отклонение от уравнения. Задача обучения будет сводится к минимизации этой ошибки.

d t(x)/d(x) = (1+t(x))(1-t(x))
d s(x)/d(x) =    s(x)·(1-s(x))

-- Производная имеет смысл градиента.

Кусочно-полиномиальные приближения функции

Мы не хотим использовать экспоненту категорически, поэтому предлагаем ориентироваться на приближенное вычисление сигмоиды или вообще заменить функцию активации на что-то приблизительно по форме напоминающее сигмоиду - ступеньку с размытыми краями. Все нормальные разработчики используют такой подход. Табличная функция активации выгядит примерно так:

// Кусочно-полиномиальные приближения функций
float activation(float x)
{
const int N=8;
   x = clamp(X_MIN, X_MAX,x);
// округляет в меньшую сторону до целого числа.
   idx = floor(x)-X_MIN;
   t  = x-floor(x);// дробная часть
   v0 = Coeff0[idx];
   v1 = Coeff1[idx];
   v2 = Coeff2[idx];
// квадратная интерполяция 
// v(t) = t*(t*v2+v1)+v0
   v = fma(t, v2,v1);
   v = fma(t, v, v0);
   return v;
}

Примерно в таком виде Intel описывает некоторую оптимизацию в собрании сочинений Intel Architectures Optimization Manual, глава 7.5.2 Fused post GEMM, Sigmoid Approximation with Minimax Polynomials. Которая оптимизация сводится к интерполяции полиномами второй степени. Этот вариант запасной. Он работает, не имеет противопоказаний, это доказано на опыте.
Можно определить функцию активации следующим образом.
На диапазоне [0+eps,1-eps] - происходит линейный рост с производной =1.
(0-eps, 0+eps) и (1-eps, 1+eps) -- сглаженный переход к насыщению - квадратным полиномом.
Назовем функцию, которая осуществляет плавный переход к насыщению Smoothie-выпрямитель. В масштабе 1.0 Smoothie-выпрямитель мы определим на интервале (-1.0,1.0) со значениями производной на конце интервала 0 и 1, соответственно.

Квадратичная интерполяция функции Smoothie-выпрямитель
F (x)  =  a2 x^2 + a1 x + a0
F'(x)  = 2a2 x   + a1
// граничные значения функции
F ( 1) =  a2 + a1 + a0 = 1
F (-1) =  a2 - a1 + a0 = 0
// производная непрерывная
F'( 1) = 2a2 + a1      = 1
F'(-1) =-2a2 + a1      = 0

a0 = 1/4, a1 = 1/2, a2 = 1/4, 

На области определения (-1,1)
SmoothieRect (x) = (x+1)(x+1)·0.25
SmoothieRect'(x) = (x+1)·0.5

В общем виде этот пример можно рассматривать, как метод вычисления коэффициентов полинома на интервале. Мы задаем производную и значение функции в каждой строчке таблицы. Таким образом рассчитываем коэффициенты интерполяции полиномом второй или третьей степени.
Позволю себе небольшое отступление для обоснования расчета коэффициентов табличного метода. Для каждого интервала нам нужно рассчитать коэффициенты полинома. Для этого нам нужно решить систему линейных уравнений полученных подстановкой граничных условий на интервале (0,1). Кто не помнит, надо посмотреть метод Гаусса-Жордана для решения систем линейных уравнений.

// Решение системы линейных уравнений.
Запишем функцию и его производную. Надо найти коэффициенты ai
F (x)  =  a3 x3 + a2 x2 + a1 x + a0
F'(x)  = 3a3 x2 +2a2 x  + a1
Шаг 1. Строим матрицу из множителей коэффициентов полинома ai, 
при заданном x и заданном значении функции bi:
  F(0) = (0, 0, 0, 1 | b0)  
 dF(0) = (0, 0, 1, 0 | b1)  
  F(1) = (1, 1, 1, 1 | b2)  
 dF(1) = (3, 2, 1, 0 | b3)  
Шаг 2. Вычитаем так чтобы получилась диагональная матрица.
b3 = b3-3b2
  F(0) = (0, 0, 0, 1 | b0)  
 dF(0) = (0, 0, 1, 0 | b1)  
  F(1) = (1, 1, 1, 1 | b2)  
 dF(1) = (0,-1,-2,-3 | b3-3b2)  
b2 = -2b2+b3
  F(0) = (0, 0, 0, 1 |  b0)  
 dF(0) = (0, 0, 1, 0 |  b1)  
  F(1) = (1, 0,-1,-2 |-2b2+ b3)  
 dF(1) = (0,-1,-2,-3 |  b3-3b2) 
b3 = b3-3b2+2b1+3b0
b2 = 2b0+b1-2b2+b3
          a3 a2 a1 a0
  F(0) = (0, 0, 0, 1 |  b0 )  
 dF(0) = (0, 0, 1, 0 |  b1 )  
  F(1) = (1, 0, 0, 0 | 2b0+ b1-2b2+b3 )  
 dF(1) = (0,-1, 0, 0 | 3b0+2b1-3b2+b3 ) 

Итого получаем: 
a0 = b0;
a1 = b1;
a3 = 2b0+ b1-2b2+b3
a2 =-3b0-2b1+3b2-b3

Далее мы рассмотрим вариант функции tanh-like активации заданный на интервале (-1,1) полиномом третьей степени.

Гладкие функции активации

Обращаю внимание на существование иных функций, smoothie-функций, которые подпадают под определение функции активации. Например, кубическая интерполяция Эрмита, функция smoothstep, S(x)=3x² - 2x³. Эта функция введена в язык OpenCL и достойна применения. Функция имеет хорошую производную S'(x) = 6(x - x²) = 6x(1-x). Даже производная похожа на сигмойду, sigmoid-like function.
Продемонстрируем вывод полиномиальной функции активации, представляем функцию активации полином третьей степени. Приравниваем производную вне области определения (-1, 1) нулю и приравниваем значение вне области определения -1 и 1 соответственно, чтобы получить tanh-like функцию.
Вычисляем коэффициенты полинома для граничных условий:

Для полинома и его производной
T (x) = a3 x3 + a2 x2 + a1 x + a0
T'(x) =3a3 x2 +2a2 x  + a1
Составляем систему уравнений для граничных условий
T ( 1) =   a3 +  a2 + a1 + a0 = 1
T (-1) = - a3 +  a2 - a1 + a0 =-1 
T'( 1) =  3a3 + 2a2 + a1      = 0
T'(-1) = -3a3 + 2a2 - a1      = 0
Из выражения для производной получаем:
a1 = -3a3, a2 = 0.
Подставляем в выражение для функции:
T ( 1) = -2a3 + a0 = 1
T (-1) =  2a3 + a0 =-1
Получаем набор коэффициентов:
a0 = 0, a1 = 3/2, a2 = 0, a3 = -1/2
Функция Tanh-like на множестве (-1,1)
T (x)= (3x - x3)1/2 = 2*Smoothstep(x + 1/2)-1
T'(x)= (1  - x2)3/2 = 3/2 (1-x)(1+x)

Интерполяция Sigmoid-like на (-1,1).
S (x)= (T(x)+1)/2 = Smoothstep(x + 1/2)
S'(x)=  T'(x)/2

На языке OpenCL C кубическую интерполяцию функции активации Sigmoid и Tanh можно выразить с использованием базовой функции smoothstep, которая может быть реализована аппаратно или хорошо оптимизирована для векторных типов. В спецификации Khronos указано, что функции реализуются с использованием инструкций fma и mad.

T(x) = 2*smoothstep(-1.0, 1.0, x+0.5)-1.0;
S(x) = smoothstep(-1.0, 1.0, x+0.5);

float smooth_tanh(float x){
  x = clamp(x, -1.0f, 1.0f);
  return (3.0f - x*x)*x*0.5f;
}
float smooth_sigm(float x){
  x = clamp(x, -1.0f, 1.0f);
  return (3.0f - x*x)*x*0.25f+0.5f;
}
float smooth_step(float edge0, float edge1, float x){
  float t;
  t = clamp((x - edge0)/(edge1 - edge0), 0, 1);
  return t * t * (3 - 2 * t );
}

Коль скоро затронули тему Smoothie-функций, можем сюда же определить смузи-функцию выпрямителя, SmoothReLU. Производная от SmoothReLU должна давать функцию SmoothStep, а производная от ReLU - функцию Step, пороговую активацию. Строго говоря, SmoothReLU должна представлять собой полином четвертой степени.

Тестирование

Задаем функцию таблицей, рассчитываем коэффициенты из таблицы, сравниваем ошибку интерполяции на интервале. Тем самым можем доказать, что функция заданная таблично работает. Затем можем экспериментировать с готовой сетью, подставлять в нее разные функции активации и сравнивать эффективность при обучении.

// расcчет коэффициентов линейной интерполяции
. . .

Заключение

Я хочу поставить току в обсуждении. Самая простая функция активации - это ее отсуствие. Это и есть самая эффективная реалиазция.

float activation_s(float x){
  return clamp(-1.0f, 1.0f, x);
}

float activation_u(float x){
  return clamp(0.0f, 1.0f, x);
}

float activation_relu(float x){
  return fmax(0.0f, x);
}

Все что нам нужно - ограничивать значение на выходе.
Кстати, чтоб развеять мистический туман вокруг встроенной функции clamp, скажу, что ее можно реализовать двумя функциями: fmax и fmin, которые в свою очередь представлены соответствующими векторными инструкциями.

// Эмуляция функции clamp
float clamp(float x, float minval, float maxval) { 
  return fmin(fmax(x, minval), maxval); 
}

Такой вид функции активации позволяет легко перейти к реализации алгоритмов в целых числах. Активация в целых числах - это просто насыщение.
Пример такой операции оптимизированной под AVX-512:

activation_u8(a,b,c,d){
// добавление константы относится к свертке.
// a = _mm512_adds_epi32(a,a0);
// b = _mm512_adds_epi32(b,b0);
// c = _mm512_adds_epi32(c,c0);
// d = _mm512_adds_epi32(d,d0);
 v0= _mm512_packus_epi32(a, b);
 v1= _mm512_packus_epi32(c, d);
 return _mm512_packus_epi16(v0, v1);
}

activation_i16(a,b){
// a = _mm512_adds_epi32(a,a0);
// b = _mm512_adds_epi32(b,b0);
 return _mm512_packs_epi32(a, b);
}