Хочу поделиться знаниями, вернее акцентировать внимание на известном факте.. Каково место цифровой обработки сигналов в коде. Хотим затолкать цифровую обработку в поток OpenCL, выполнять обработку на потоке данных.
При этом не дает покоя одна мысль. Мы хотим получить наивысшую скорость работы и малые задержки. Поэтому мы каждый алгоритм DSP хотим разделить на две части. В первой части рассчитываем результат за минимальное число операций, во второй обновляем значения переменных. Я начну писать, потом видно будет.
В разделе DSP есть два вида фильтров: IIR- и FIR- фильтры. Прежде всего, оговорюсь все это относится к анализу LTI-систем, для которых можно описать передаточную функцию Y(s)=H(s)X(s) в непрерывном виде и далее перейти к дискретному виду передаточной функции H(z) путем замены переменной s←2/T(z-1)/(z+1). Передаточную функцию можно представить в виде отношения полиномов B(z)/A(z). Т.е.в виде дроби (дробно-рациональной функции) - сверху и снизу дроби полином z. Причем буква Z-1 на самом деле представляет из себя оператор задержки в дискретном по времени процессе. Как вообще люди в процессе своего образования доходят до этого - загадка. Думаю все сознательные электронщики и программисты должны это знать, но полагаю мало, кто знает. Наше образование не было полным в том виде, в каком оно может служить инструментом программиста или электронщика. Статья для избранных. На самом деле я уже начинаю сомневаться, что вообще этому учат. Когда-то учили анализу систем, учили передаточным функциям. Предлагаю, сейчас найти учебник на английском (по теме Linear time-invariant system и Digital Signal Processing). Для работы, чтобы получить готовый набор коэффициентов использую GNU Octave или MATLAB с модулем Signal, он умеет готовить матрицы коэффициентов. Использую конспекты лекций по курсу DSP & Digital Filters, потому что мне это близко и понятно, именно в таком виде. Автор курса ссылается на учебник.
[#] "Digital Signal Processing" Sanjit K. Mitra, 4th edition, McGraw Hill, 2011. ISBN 0071289461
Для стационарных систем (LTI) передаточная функция — это дробно-рациональная функция комплексной переменной s. Тернистый путь познания лежит через преобразования Фурье и Лапласа. Однако более короткий путь можно найти через дифференциальные уравнения в конечных разностях, только этот путь неведом выпускникам со специальностью кибернетика, так учат физиков. У меня в образовании был курс ТФКП(теория функции комплексного переменного) и курс математической физики (который символизирует наезд дельта функцией на уравнения), от которого ничего тут использовать не буду.
1) Систему можно представить в виде дробно рациональной функции N-ого порядка в странном пространстве наполненном операторами задержки и умножителями, -- это понятно программисту. Причем порядок числителя не выше чем у знаменателя. 2) Безумную дробь можно разложить на полюса и нули(полюса - это решения полинома в знаменателе, нули - решение полинома в числителе), путем факторизации полинома(еще одно умное слово - разложить на скобки, - так говорят в школе). Длинную дробно рациональную функцию большого порядка можно представить в виде суммы или произведения этих самых дробно-рациональных функций второго порядка. (точка!! - никакой больше теории, только картинки).
Иногда я чувствую, что являюсь хранителем некоего сокровенного невербального знания :). Могу доказать теорему не произнося слова, а рисуя только квадратики, треугольнички и стрелочки. Передаточные функции в дискретном пространстве можно строить в виде графов и представлять математические преобразования над функциям, как тождественные преобразования графов. Граф в точности отражает архитектуру программной или аппаратной реализации алгоритма цифровой обработки. На картинке буквой Z обозначаем оператор задержки, фактически это будет переменная (буфер, в аппаратуре - D-триггер), в которой хранится значение с предыдущего шага обработки.
Рис.1 Биквадратный фильтр. Прямое представление 1-типа DF1 (слева) и прямое представление 2-типа DF2 (справа)
Рисунок #1 получен путем прямой записи выраженияB(z)X = (b0+b1·z-1+b2·z-2)X и затем выражения
A(z)Y = (1-a1·z-1-a2·z-2)Y , где z-1 - оператор задержки на такт.
В первом случае (DF1)сложность, 5 умножений и 4 сложения: 5m+4a. Во втором (DF2) сложность та же, но для получения хранения промежуточных значений достаточно всего двух регитров Z.
Рис.2 Биквадратный фильтр. Прямое представление 2-типа DF2 (слева) и прямое представление второго типа транспонированное DF2T (справа)
Y = b0·X+z0
От входа X до выхода Y одно суммирование и одно умножение. Сложность первого прохода: 1m+1a. Этот проход совершается в той же самой математике, что и процесс свертки слоя нейронной сети.
К чему все это?. А, к нейролизации цифровой обработки сигналов в дискурсе для непосвещенных. Все что ниже первой линии будем считать частью процесса обучения, т.е. расчитывать и обновлять значения Z будем на втором проходе сети.
Какие у нас открываются возможности при использовании параллельной архитектуры. Правильно, фильтры могли бы считать паралельно, а не последовательно. Привычное разложение передаточной функции высокого порядка - в каскад (произведение) фильтров второго порядка. Каскад - это последовательная обработка фильтров, предполагает загрузку одного ядра/потока. Возможно представление в виде суммы, можно разложить в сумму фильтров первого и второго порядка. Cмотрю на структуру каскада фильтров. Каскад расчитывается, как sum(z1k+b0kX). Переобозначим переменную, S=sum(z1k) -- сумму можно расчитывать на втором проходе.
Рис.3 Каскад биквадратных фильтров.
Получаем финально такой результат: каскад фильтров можно представить на первом проходе Y =Z+ gX. Весь фильтр в одно действие!
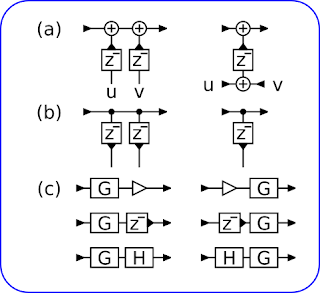
Рис.4 Тождественные преобразования. a) замена переменных, b) объединение идентичных буферов, c) свойство линейности преобразования.
Предлагаю для практики проделать преобразования фильтров. На рисунке #5 привожу последовательное, шаг за шагом, преобразование фильтра Allpass первого порядка из одной формы в другую. Считается, что каждый студент прослушавший курс лекций должен понимать, как проделать подобный переход.
На рисунке #6 представлена одиночная операция транспонирования над одним каскадом фильтра FIR.
Ниже пример реализации FIR фильтра. Также разделен на два прохода.
В разделе DSP есть два вида фильтров: IIR- и FIR- фильтры. Прежде всего, оговорюсь все это относится к анализу LTI-систем, для которых можно описать передаточную функцию Y(s)=H(s)X(s) в непрерывном виде и далее перейти к дискретному виду передаточной функции H(z) путем замены переменной s←2/T(z-1)/(z+1). Передаточную функцию можно представить в виде отношения полиномов B(z)/A(z). Т.е.в виде дроби (дробно-рациональной функции) - сверху и снизу дроби полином z. Причем буква Z-1 на самом деле представляет из себя оператор задержки в дискретном по времени процессе. Как вообще люди в процессе своего образования доходят до этого - загадка. Думаю все сознательные электронщики и программисты должны это знать, но полагаю мало, кто знает. Наше образование не было полным в том виде, в каком оно может служить инструментом программиста или электронщика. Статья для избранных. На самом деле я уже начинаю сомневаться, что вообще этому учат. Когда-то учили анализу систем, учили передаточным функциям. Предлагаю, сейчас найти учебник на английском (по теме Linear time-invariant system и Digital Signal Processing). Для работы, чтобы получить готовый набор коэффициентов использую GNU Octave или MATLAB с модулем Signal, он умеет готовить матрицы коэффициентов. Использую конспекты лекций по курсу DSP & Digital Filters, потому что мне это близко и понятно, именно в таком виде. Автор курса ссылается на учебник.
[#] "Digital Signal Processing" Sanjit K. Mitra, 4th edition, McGraw Hill, 2011. ISBN 0071289461
Для стационарных систем (LTI) передаточная функция — это дробно-рациональная функция комплексной переменной s. Тернистый путь познания лежит через преобразования Фурье и Лапласа. Однако более короткий путь можно найти через дифференциальные уравнения в конечных разностях, только этот путь неведом выпускникам со специальностью кибернетика, так учат физиков. У меня в образовании был курс ТФКП(теория функции комплексного переменного) и курс математической физики (который символизирует наезд дельта функцией на уравнения), от которого ничего тут использовать не буду.
1) Систему можно представить в виде дробно рациональной функции N-ого порядка в странном пространстве наполненном операторами задержки и умножителями, -- это понятно программисту. Причем порядок числителя не выше чем у знаменателя. 2) Безумную дробь можно разложить на полюса и нули(полюса - это решения полинома в знаменателе, нули - решение полинома в числителе), путем факторизации полинома(еще одно умное слово - разложить на скобки, - так говорят в школе). Длинную дробно рациональную функцию большого порядка можно представить в виде суммы или произведения этих самых дробно-рациональных функций второго порядка. (точка!! - никакой больше теории, только картинки).
Иногда я чувствую, что являюсь хранителем некоего сокровенного невербального знания :). Могу доказать теорему не произнося слова, а рисуя только квадратики, треугольнички и стрелочки. Передаточные функции в дискретном пространстве можно строить в виде графов и представлять математические преобразования над функциям, как тождественные преобразования графов. Граф в точности отражает архитектуру программной или аппаратной реализации алгоритма цифровой обработки. На картинке буквой Z обозначаем оператор задержки, фактически это будет переменная (буфер, в аппаратуре - D-триггер), в которой хранится значение с предыдущего шага обработки.
Рис.1 Биквадратный фильтр. Прямое представление 1-типа DF1 (слева) и прямое представление 2-типа DF2 (справа)
Рисунок #1 получен путем прямой записи выражения
В первом случае (DF1)сложность, 5 умножений и 4 сложения: 5m+4a. Во втором (DF2) сложность та же, но для получения хранения промежуточных значений достаточно всего двух регитров Z.
Рис.2 Биквадратный фильтр. Прямое представление 2-типа DF2 (слева) и прямое представление второго типа транспонированное DF2T (справа)
Метод Транспонирования цифрового фильтра:
1) Меняем направление обхода, все стрелочки и треугольники разворачиваем.
2) Слева будет выход, справа вход. Меняем местами буквы X и Y.
3) Разворачиваем буферы Z.
4) Где были узлы ставим "плюсик", где плюсики - ставим узел.
К чему все это?. А, к нейролизации цифровой обработки сигналов в дискурсе для непосвещенных. Все что ниже первой линии будем считать частью процесса обучения, т.е. расчитывать и обновлять значения Z будем на втором проходе сети.
Какие у нас открываются возможности при использовании параллельной архитектуры. Правильно, фильтры могли бы считать паралельно, а не последовательно. Привычное разложение передаточной функции высокого порядка - в каскад (произведение) фильтров второго порядка. Каскад - это последовательная обработка фильтров, предполагает загрузку одного ядра/потока. Возможно представление в виде суммы, можно разложить в сумму фильтров первого и второго порядка. Cмотрю на структуру каскада фильтров. Каскад расчитывается, как sum(z1k+b0kX). Переобозначим переменную, S=sum(z1k) -- сумму можно расчитывать на втором проходе.
Рис.3 Каскад биквадратных фильтров.
Получаем финально такой результат: каскад фильтров можно представить на первом проходе Y =Z+ gX. Весь фильтр в одно действие!
// Алгоритм
float cascaded_iir_df2t(float x){
// первый проход
y = g*x+s;
return y;
}
float cascaded_iir_df2t_update(float x){
// второй проход, вычисляем s
s=0;
x=g*x;
for (i=0; i<len; i++){
y = x+z1[i];
z1[i] = b1[i]*x - a1[i]*y + z2[i];
z2[i] = b2[i]*x - a2[i]*y;
s+=z1[i];
x = y;
}
return s;
}
Преобразования фильтров
Рис.4 Тождественные преобразования. a) замена переменных, b) объединение идентичных буферов, c) свойство линейности преобразования.
Предлагаю для практики проделать преобразования фильтров. На рисунке #5 привожу последовательное, шаг за шагом, преобразование фильтра Allpass первого порядка из одной формы в другую. Считается, что каждый студент прослушавший курс лекций должен понимать, как проделать подобный переход.
Рис.5 Преобразования фильтра Allpass
На рисунке #6 представлена одиночная операция транспонирования над одним каскадом фильтра FIR.
Рис.6 Преобразования фильтра FIR. Транспонирование каскада.
Векторизация фильтров
Следующий пункт - оптимизация под оборудование. Возможно будет лучше считать в векторном типе с использованием явной векторизации. Исходно мы используем транспонированную форму фильтра.
Рис.7 Прямая и транспонированная форма FIR-фильтра
Ниже пример реализации FIR фильтра. Также разделен на два прохода.
// FIR фильтр с явной векторизацией
float fir_dft(float x){
y = g*x+z.s0;
return y;
}
float4 fir_dft_update(float4 z, float x){
Z0=(0.0f);
z = shuffle2(z,Z0, (int4){1,2,3,4});
z =z + H*x;
return z;
}






Комментариев нет:
Отправить комментарий